题目内容
已知函数f（x）=| 3 |
| A、周期为4的奇函数 |
| B、周期为4的偶函数 |
| C、周期为2π的非奇非偶函数 |
| D、周期为4的非奇非偶函数 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质,解三角形
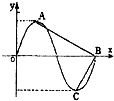
分析：先表示出函数的最小正周期，则A，B，C的坐标可分别表示出来，进而根据∠ABC=90°判断出两直线斜率的乘积为-1求得ω，则函数最小正周期可得．进而求得f（x+1）推断出函数的奇偶性．
解答：
解：依题意T=
，
则A点坐标为（
，
），B的坐标为（
，0），C坐标为（
，-
），
∵∠ABC=90°，
∴kAB•kBC=
•
=-1，求得ω=
，
∴T=
=4，
∴f（x）=
sinωx=
sin（
x），
∴f（x+1）=
sin（
+
）=
cos
，
∴f（x+1）为偶函数，
故选B．
| 2π |
| ω |
则A点坐标为（
| π |
| 2ω |
| 3 |
| 2π |
| ω |
| 3π |
| 2ω |
| 3 |
∵∠ABC=90°，
∴kAB•kBC=
| ||||
|
| ||||
|
| π |
| 2 |
∴T=
| 2π |
| ω |
∴f（x）=
| 3 |
| 3 |
| π |
| 2 |
∴f（x+1）=
| 3 |
| πx |
| 2 |
| π |
| 2 |
| 3 |
| πx |
| 2 |
∴f（x+1）为偶函数，
故选B．
点评：本题主要考查了三角函数图象和性质．考查了学生对基础知识的掌握．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中，既是偶函数又在区间（-∞，0）上单调递增的是（ ）
| A、y=x2 | ||
| B、y=x3 | ||
| C、y=tanx | ||
D、y=
|
在平面直角坐标系xOy中，角α的终边与单位圆交于点A，点A在第二象限，且点A的横坐标与纵坐标之比为-
，则
的值为（ ）
| 1 |
| 2 |
| cos2α-sin2α |
| sin2α+2cos2α |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
设变量x，y满足约束条件
，则“m≥2”是“目标函数z=3x-2y的最大值不小于5”的（ ）
|
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
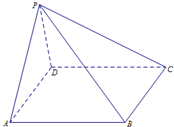已知四棱锥P-ABCD，底面ABCD是边长为2的菱形，且∠BAD=60°，PA=PD=2，平面PAD⊥平面ABCD，则它的正视图的面积是（ ）执行如图所示的程序框图，若输出的结果是26，则在①处应填入的条件是（ ）
| A、K＞2？ | B、K＞3？ |
| C、K＞4？ | D、K＞5？ |