题目内容
2．下列函数中既是奇函数，又在区间（-1，1）上是增函数的为（ ）| A． | y=|x+1| | B． | y=sinx | C． | y=2x+2-x | D． | y=lnx |
分析 根据奇函数、偶函数的定义，以及正弦函数的单调性即可判断每个选项的正误，从而找出正确选项．
解答 解：A．x=-1时，y=0；
x=1时，y=2；
∴函数y=|x+1|不是奇函数；
∴该选项错误；
B．y=sinx为奇函数，且在（-1，1）上是增函数；
∴该选项正确；
C．y=2x+2-x为偶函数，不是奇函数；
∴该选项错误；
D．y=lnx为非奇非偶函数；
∴该选项错误．
故选B．
点评 考查奇函数和偶函数的定义，以及对数函数的奇偶性，正弦函数的单调性．
练习册系列答案
相关题目
，
，
B．
C．
D．
14．函数f（x）=ax3+lnx在区间（0，+∞）上不是单调函数，则a的取值范围是（ ）
| A． | （-1，1） | B． | （-1，2） | C． | （-∞，0） | D． | （0，+∞） |
10．函数y=-$\frac{2}{x}$的单调增区间为（ ）
| A． | [0，+∞） | B． | （-∞，0） | C． | （-∞，0），（0，+∞） | D． | （-∞，+∞） |
17．若实数a，b满足$\frac{1}{a}+\frac{4}{b}=\sqrt{ab}$，则ab的最小值为（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
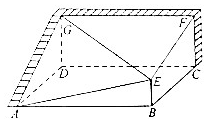要利用现有的两面残墙，呈直角三角形墙ADG和矩形墙DCFG搭建成一个暖棚（如图所示），所立柱子EB垂直于暖棚底面ABCD，其余四面计划用薄膜覆盖，已知底面ABCD是边长为2$\sqrt{6}$cm的正方形，且GD=2m，EB=1m．