题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,且满足右焦点(c,0)到直线x=
的距离为
,
(Ⅰ) 求椭圆的方程;
(Ⅱ)已知A(2,-1),过原点且斜率为k(k>0)的直线l与椭圆交于P、Q两点,求△APQ面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 3 |
(Ⅰ) 求椭圆的方程;
(Ⅱ)已知A(2,-1),过原点且斜率为k(k>0)的直线l与椭圆交于P、Q两点,求△APQ面积的最大值.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)设右焦点为(c,0)(c>0)通过|c-
|=
,求出c,利用离心率求出a,然后求解b,即可求出椭圆的标准方程.
(2)设P(x1,y1),Q(x2,y2)将直线l方程:y=kx与椭圆方程联立消y得求出x,利用弦长公式,以及点到直线的距离求出三角形的高,表示出三角形的面积,利用基本不等式求出面积的最大值.
| 3 |
| 3 |
(2)设P(x1,y1),Q(x2,y2)将直线l方程:y=kx与椭圆方程联立消y得求出x,利用弦长公式,以及点到直线的距离求出三角形的高,表示出三角形的面积,利用基本不等式求出面积的最大值.
解答:
解:(1)设右焦点为(c,0)(c>0)依题意可知|c-
|=
,
∴c=2
或c=0(舍去),…(2分)
又∵离心率为
,∴a=4故b2=a2-c2=4,
因此椭圆的方程为:
+
=1;…(4分)
(2)设P(x1,y1),Q(x2,y2),
将直线l方程:y=kx与椭圆方程联立消y得(1+4k2)x2-16=0,所以x2=
…(6分)
∴|PQ|=
|x2-x1|=
×2×
,…(8分)
又∵点A到直线l的距离d=
,…(9分)
故△APQ的面积=
|PQ|•d=4×
=4×
=4×
=4×
,…(11分)
当k>0时,
+4k≥4(当且仅当k=
时,取等号).
故△APQ的面积有最大值4
.…(12分)
| 3 |
| 3 |
∴c=2
| 3 |
又∵离心率为
| ||
| 2 |
因此椭圆的方程为:
| x2 |
| 16 |
| y2 |
| 4 |
(2)设P(x1,y1),Q(x2,y2),
将直线l方程:y=kx与椭圆方程联立消y得(1+4k2)x2-16=0,所以x2=
| 16 |
| 1+4k2 |
∴|PQ|=
| 1+k2 |
| 1+k2 |
|
又∵点A到直线l的距离d=
| |2k+1| | ||
|
故△APQ的面积=
| 1 |
| 2 |
| |2k+1| | ||
|
|
=4×
1+
|
1+
|
当k>0时,
| 1 |
| k |
| 1 |
| 2 |
故△APQ的面积有最大值4
| 2 |
点评:本题考查椭圆的标准方程的求法,直线与椭圆的位置关系,椭圆方程的综合应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
在3与27之间插入7个数,使它们成为等差数列,则插入的7个数的第四个数是( )
| A、18 | B、9 | C、12 | D、15 |
如图所示,在平行六面体ABCD-A1B1C1D1中,点E为上底面对角线A1C1的中点,若
=
+x
+y
,则( )
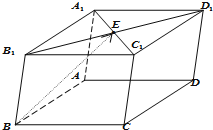
| BE |
| AA1 |
| AB |
| AD |

A、x=-
| ||||
B、x=
| ||||
C、x=-
| ||||
D、x=
|
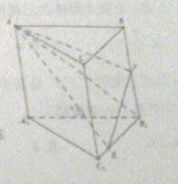 如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.
如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.