题目内容
对于任意的x∈R，a2x2+ax+1＞0恒成立，则a的取值范围是（ ）
| A、a＜0 | B、a≤0 |
| C、a＞0 | D、a∈R |
考点：函数恒成立问题
专题：计算题,函数的性质及应用
分析：分a=0，a≠0两种情况进行讨论，当a=0时易判断；当a≠0时由△＜0，即可得出结论．
解答：
解：（1）当a=0时，不等式为1＞0，恒成立；
（2）当a≠0时，设f（x）=a2x2+ax+1，其图象开口向上，要满足题意，则△=a2-4a2＜0，恒成立．
综上，a的取值范围为a∈R．
故选：D．
（2）当a≠0时，设f（x）=a2x2+ax+1，其图象开口向上，要满足题意，则△=a2-4a2＜0，恒成立．
综上，a的取值范围为a∈R．
故选：D．
点评：本题考查函数恒成立问题，考查数形结合思想，关于二次函数恒成立问题，往往采取数形结合思想进行解决．
练习册系列答案
相关题目
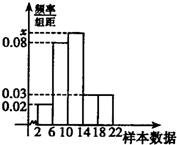为了调查学生每天零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．样本容量1000的频率分布直方图如图所示，则样本数据落在[6，14）内的频数为（ ）| A、780 | B、660 |
| C、680 | D、460 |
已知sinα=-
，则cos（
-α）的值等于（ ）
| 1 |
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列统计图中，未丢失数据的统计图是（ ）
| A、茎叶图 | B、条形图 |
| C、折线图 | D、扇形图 |
若0＜y＜x＜
，且tan2x=3tan（x-y），则x+y的可能取值是（ ）
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列语句不是命题的是（ ）
| A、新津中学是一所国家级示范校 |
| B、如果这道题做不好，那么这次考试成绩不理想 |
| C、?x0∈R，使得lnx0＜0 |
| D、走出去！ |
命题“存在x∈Z，使x3-2x+m≥0”的否定是（ ）
| A、存在x∈Z，使x3-2x+m≤0 |
| B、不存在x∈Z，使x3-2x+m≥0 |
| C、对任意的x∈Z，使x3-2x+m≥0 |
| D、对任意的x∈Z，使x3-2x+m＜0 |