题目内容
已知两正数x、y满足x+y=2,求
-4x的取值范围.
| x |
| y |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:由x+y=2,x,y>0,则
+
=
+
,展开后运用基本不等式,即可得到取值范围.
| x |
| y |
| 4 |
| x |
| x |
| y |
| 2(x+y) |
| x |
解答:
解:∵x+y=2,x,y>0,
∴
+
=
+
=2+
+
≥2+2
=2+2
.
当且仅当
=
即x=4-2
,y=2
-2时,上式取等号,
则
+
的取值范围是:[2+2
,+∞).
∴
| x |
| y |
| 4 |
| x |
| x |
| y |
| 2(x+y) |
| x |
| x |
| y |
| 2y |
| x |
|
| 2 |
当且仅当
| x |
| y |
| 2y |
| x |
| 2 |
| 2 |
则
| x |
| y |
| 4 |
| x |
| 2 |
点评:本题考查基本不等式的运用,注意掌握常数代换法,是迅速解题的关键,注意等号成立的条件,属于中档题.

练习册系列答案
相关题目
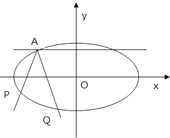 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).