题目内容
设曲线f（x）=2ax3-a在点（1，a）处的切线与直线2x-y+1=0平行，则实数cos（a+
）的值为 ．
| π |
| 3 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求出函数f（x）=2ax3-a的导数，进而求得函数在x=1处得导数为6a，再利用两直线平行的条件可求出a的值．
解答：
解：f（x）=2ax3-a的导数为f′（x）=6ax2．
则在x=1处的切线的斜率为f′（1）=6a．
由于f（x）=2ax3-a在点（1，a）处的切线与直线2x-y+1=0平行．
而直线2x-y+1=0的斜率为2．
即有6a=2，
解得a=
．
故答案为
．
则在x=1处的切线的斜率为f′（1）=6a．
由于f（x）=2ax3-a在点（1，a）处的切线与直线2x-y+1=0平行．
而直线2x-y+1=0的斜率为2．
即有6a=2，
解得a=
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题主要考查学生会利用导数求曲线在过某点处的切线方程的斜率和两直线平行的判断，以及对导数的综合掌握，解题时注意转化思想的运用，属于基础题．
练习册系列答案
相关题目
把函数y=-3cos（2x+
）的图象向右平移m（m＞0）个单位，所得图象关于y轴对称，则m的值可以是 （ ）
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=
在R上为增函数，则a的取值范围是（ ）
|
| A、（1，2] |
| B、（1，+∞） |
| C、[1，+∞） |
| D、（1，2） |
复数(
)2013（i为虚数单位）等于（ ）
| 1+i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
已知数列{an}满足a1=0，an+1=an+2n，那么a2015的值是（ ）
| A、2 012×2 013 |
| B、2 014×2 015 |
| C、2 0142 |
| D、2 013×2 014 |
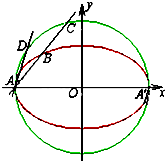如图，已知椭圆E1：