题目内容
12.某几何体的三视图如图所示,则该几何体的体积为( )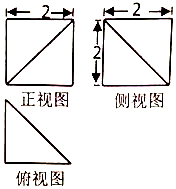
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $2\sqrt{2}$ | D. | 4 |
分析 由三视图可知:该几何体为四棱锥P-ABCD.其中底面ABCD是矩形,AB=2.底面ABCD⊥侧面PAD,PD=PA=2,PA⊥PD.取AD的中点O,连接PO,则PO⊥底面ABCD,PO=$\sqrt{2}$,AD=2$\sqrt{2}$.
解答 解:由三视图可知:该几何体为四棱锥P-ABCD.
其中底面ABCD是矩形,AB=2.底面ABCD⊥侧面PAD,PD=PA=2,PA⊥PD.
取AD的中点O,连接PO,则PO⊥底面ABCD,PO=$\sqrt{2}$,AD=2$\sqrt{2}$.
∴该几何体的体积V=$\frac{1}{3}×2×2\sqrt{2}×\sqrt{2}$=$\frac{8}{3}$.
故选:A.
点评 本题考查了四棱锥的三视图、四棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如果过原点的直线l与圆x2+(y-4)2=4切于第二象限,那么直线l的方程是( )
| A. | $y=\sqrt{3}x$ | B. | $y=-\sqrt{3}x$ | C. | y=2x | D. | y=-2x |
17.函数y=sinx-cosx,则f'(π)的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | π |
2.已知集合A={x∈N|4x-x2≥0},B={x∈N|log2(x+1)≥2},则A∩B等于( )
| A. | {2,3} | B. | {3,4} | C. | {4,5} | D. | {5,6} |