题目内容
9.如果过原点的直线l与圆x2+(y-4)2=4切于第二象限,那么直线l的方程是( )| A. | $y=\sqrt{3}x$ | B. | $y=-\sqrt{3}x$ | C. | y=2x | D. | y=-2x |
分析 由已知得圆心坐标为(0,4),半径长为2.因为直线斜率存在.设直线方程为 y=kx,根据圆心到直线的距离等于半径,确定k的值,从而求出直线方程
解答 解:圆心坐标为(0,4),半径长为2.
由直线过原点,当直线斜率不存在时,不合题意,
设直线方程为;y=kx,即kx-y=0.
则圆心到直线的距离d=$\frac{4}{\sqrt{1+{k}^{2}}}$=r=2
化简得:k2=3
又∵切点在第二象限,∴$k=-\sqrt{3}$
∴直线方程为;y=-$\sqrt{3}$x
故选:B.
点评 本题考查直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题

练习册系列答案
相关题目
19.已知直线l1:ax+2y=0与直线l2:x+(a-1)y+a2-1=0平行,则实数a的值是( )
| A. | -1或2 | B. | 0或1 | C. | -1 | D. | 2 |
20.已知一个几何体的三视图如图所示,则该几何体的表面积为( )
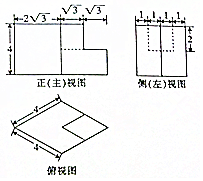

| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |
17.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1,则( )
| A. | $f(6)<f(-7)<f(\frac{11}{2})$ | B. | $f(6)<f(\frac{11}{2})<f(-7)$ | C. | $f(-7)<f(\frac{11}{2})<f(6)$ | D. | $f(\frac{11}{2})<f(-7)<f(6)$ |
12.某几何体的三视图如图所示,则该几何体的体积为( )
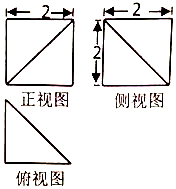

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $2\sqrt{2}$ | D. | 4 |