题目内容

17．函数y=sinx-cosx，则f'（π）的值是（　　）
A．-1B．0C．1D．π

分析 根据题意，由函数的解析式计算可得f′（x）=cosx+sinx，令x=π计算可得f'（π），即可得答案．

解答 解：根据题意，f（x）=sinx-cosx，
则f′（x）=cosx+sinx，f'（π）=cosπ+sinπ=-1；
故选：A．

点评 本题考查导数的计算，关键要掌握导数的计算公式．

练习册系列答案
相关题目
13．已知定义在R上的函数f（x）为增函数，当x1+x2=1时，不等式f（x1）+f（0）＞f（x2）+f（1）恒成立，则实数x1的取值范围是（　　）
A．（-∞，0）B．$（0，\frac{1}{2}）$C．（$\frac{1}{2}$，1）D．（1，+∞）
14．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，右焦点为F，点B（0，1）在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点$（1，\frac{2}{k}]$的直线交椭圆C于M，N两点，交直线x=2于点P，设$\overrightarrow{PM}=λ\overrightarrow{MF}$，$\overrightarrow{PN}=μ\overrightarrow{NF}$，求证：λ+μ为定值．
5．tan330°=-$\frac{\sqrt{3}}{3}$．
12．某几何体的三视图如图所示，则该几何体的体积为（　　）
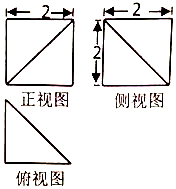
A．$\frac{8}{3}$B．$\frac{4}{3}$C．$2\sqrt{2}$D．4
2．等差数列{an}的前n项和为Sn，且$\frac{S_6}{S_3}=4$，则$\frac{S_9}{S_6}$=（　　）
A．$\frac{9}{4}$B．$\frac{2}{3}$C．$\frac{5}{3}$D．4
9．已知A，B是圆C1：x2+y2=1上的动点，AB=$\sqrt{3}$，P是圆C2：（x-3）2+（y-4）2=1上的动点，则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围为[7，13]．
6．已知圆M：x2+y2-2ay=0（a＞0）截直线x+y=0所得线段的长度是2，则圆M与圆N：（x-1）2+（y-1）2=1的位置关系是（　　）
A．内切B．相交C．外切D．相离
7．（x-1）（$\frac{1}{x}$+x）6的展开式中的一次项系数是（　　）
A．5B．14C．20D．35

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网