题目内容
1．设m为实数，函数f（x）=x3-x2-x+m．（1）求f（x）的极值点；
（2）如果曲线y=f（x）与x轴仅有一个交点，求实数m的取值范围．
分析 （1）求出函数的导数，解关于导函数的方程，求出函数的极值点即可；
（2）问题转化为$f（-\frac{1}{3}）＜0$或f（1）＞0，求出m的范围即可．
解答 解：（1）函数y=f（x）的定义域为R，
令f'（x）=3x2-2x-1=0，解得x=1或$x=-\frac{1}{3}$，
易知y=f（x）的极大值点为-$\frac{1}{3}$，极小值点为1．
（2）由（1）知：欲使曲线y=f（x）与x轴仅有一个交点，
则$f（-\frac{1}{3}）＜0$或f（1）＞0，
可得$m＜-\frac{5}{27}$或m＞1．
点评 本题考查了函数的极值问题，考查导数的应用以及转化思想，是一道中档题．
练习册系列答案
相关题目
17．已知定义在R上的奇函数f（x）满足f（x+2）=-f（x），当x∈[0，1]时，f（x）=2x-1，则（ ）
| A． | $f（6）＜f（-7）＜f（\frac{11}{2}）$ | B． | $f（6）＜f（\frac{11}{2}）＜f（-7）$ | C． | $f（-7）＜f（\frac{11}{2}）＜f（6）$ | D． | $f（\frac{11}{2}）＜f（-7）＜f（6）$ |
12．某几何体的三视图如图所示，则该几何体的体积为（ ）
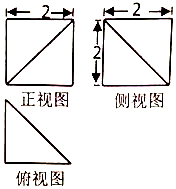
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | $2\sqrt{2}$ | D． | 4 |