题目内容
7.设集合A={x|x2-3x-4<0},B={x|-3<x<1}.(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
分析 (1)由一元二次不等式的解法可得集合A,进而由集合交集的意义计算可得答案;
(2)由一元二次不等式与一元二次方程的关系可得-3和1是方程2x2+ax+b=0的两根,进而由根与系数的关系的关系可得$\left\{\begin{array}{l}{(-3)+1=\frac{a}{2}}\\{(-3)×1=\frac{b}{2}}\end{array}\right.$,解可得a、b的值,即可得答案.
解答 解:(1)根据题意,A={x|x2-3x-4<0}={x|-1<x<4},
则A∩B={x|-1<x<1};
(2)若2x2+ax+b<0的解集为B={x|-3<x<1}.
则-3和1是方程2x2+ax+b=0的两根,
必有$\left\{\begin{array}{l}{(-3)+1=\frac{a}{2}}\\{(-3)×1=\frac{b}{2}}\end{array}\right.$,解可得a=3,b=4;
故a=4,b=-6.
点评 本题考查一元二次不等式的解法,涉及集合交集的运算,

练习册系列答案
相关题目
12.某几何体的三视图如图所示,则该几何体的体积为( )
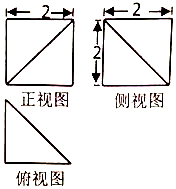

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $2\sqrt{2}$ | D. | 4 |
19.已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
据此估计,该运动员三次投篮恰有两次命中的概率为( )
| 137 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
| 431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
| A. | 0.40 | B. | 0.30 | C. | 0.35 | D. | 0.25 |