题目内容
14.已知a+b+c=1,证明:(a+1)2+(b+1)2+${({c+1})^2}≥\frac{16}{3}$.分析 利用柯西不等式,即可证明
解答 证明:由柯西不等式可得(1+1+1)[(a+1)2+(b+1)2+(c+1)2]≥(a+1+b+1+c+1)2,
∵a+b+c=1,
∴(a+1)2+(b+1)2+(c+1)2≥$\frac{16}{3}$,当且仅当a=b=c=$\frac{1}{3}$时取等号,
问题得以证明
点评 本题考查了不等式的证明,属于基础题

练习册系列答案
相关题目
4.已知函数f(x)=lnx-a(x-1),a∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当x>0时,f(x)≤0恒成立;
(1)求a的值;
(2)若f(x1)=f(x2),x1≠x2,求证:x1+x2>2.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当x>0时,f(x)≤0恒成立;
(1)求a的值;
(2)若f(x1)=f(x2),x1≠x2,求证:x1+x2>2.
5.如图,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$=( )
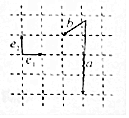

| A. | 3$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | -2$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$ | C. | $\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ |
19.若a,b∈R,i为虚数单位,且(2a+i)i=b+i,则a,b的值分别是( )
| A. | a=$\frac{1}{2}$,b=1 | B. | a=$\frac{1}{2}$,b=-1 | C. | a=-$\frac{1}{2}$,b=1 | D. | a=-$\frac{1}{2}$,b=-1 |
3.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数y=f′(x)的导函数,若方程f″(x0)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”,已知函数f(x)=3x+asinx-bcosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
4.在△ABC中$A=\frac{π}{3},b+c=4,E、F$为边BC的三等分点,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为( )
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |