题目内容
15.若命题“?x0∈R,使得x2+2x+a≤0”是假命题,则实数a的取值范围是(1,+∞).分析 命题“?x0∈R,使得x2+2x+a≤0”是假命题,则命题“?x∈R,使得x2+2x+a>0”是真命题,可得:△<0,解出a的范围.
解答 解:命题“?x0∈R,使得x2+2x+a≤0”是假命题,
则命题“?x∈R,使得x2+2x+a>0”是真命题,
∴△=4-4a<0,解得a>1.
实数a的取值范围是:(1,+∞).
故答案为:(1,+∞).
点评 本题考查了简易逻辑的判定方法、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.如图,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$=( )
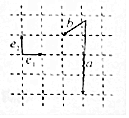

| A. | 3$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | -2$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$ | C. | $\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ |
3.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数y=f′(x)的导函数,若方程f″(x0)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”,已知函数f(x)=3x+asinx-bcosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
10.某高校通过调查在发现该校毕业生的学习成绩与就业情况具有线性相关关系,现对5名毕业生的数据进行分析,他们的专业课成绩xi及现在的工作年薪yi情况如下:
(1)根据表中数据,计算专业课成绩与年薪的线性相关系数;
(2)求出专业课成绩与年薪关系的线性回归方程,并预测专业课成绩为9.6分的学生毕业后的年薪;
(3)若再从这5名毕业生中随机抽取2名进行详细调查,求恰有一名毕业生的专业课成绩不少于9分的概率.附:r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}•\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n{\overline{y}}^{2}}}$,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 专业课成绩xi(分) | 7 | 7 | 8 | 9 | 9 |
| 年薪yi(万元) | 10 | 12 | 14 | 14 | 15 |
(2)求出专业课成绩与年薪关系的线性回归方程,并预测专业课成绩为9.6分的学生毕业后的年薪;
(3)若再从这5名毕业生中随机抽取2名进行详细调查,求恰有一名毕业生的专业课成绩不少于9分的概率.附:r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}•\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n{\overline{y}}^{2}}}$,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
4.在△ABC中$A=\frac{π}{3},b+c=4,E、F$为边BC的三等分点,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为( )
| A. | $\frac{{9\sqrt{3}}}{2}$ | B. | $\frac{8}{3}$ | C. | $\frac{26}{9}$ | D. | 3 |
7.设U=R,A={x|mx2+8mx+21>0},∁UA=∅,则m的取值范围是( )
| A. | [0,$\frac{21}{16}$) | B. | {0}∪($\frac{21}{16}$,+∞) | C. | (-∞,0] | D. | (-∞,0]∪($\frac{21}{16}$,+∞) |