题目内容
17．
运行如图所示程序框图，若输入值x∈[-2，2]，则输出值y的取值范围是[-1，6]．
分析 运行如图所示程序框图知该程序的功能是输出函数y=$\left\{\begin{array}{l}{-3x，x＜0}\\{x（x-2），x≥0}\end{array}\right.$；根据x的取值范围，求出y的取值范围即可．
解答 解：运行如图所示程序框图，知该程序的功能是：
输出函数y=$\left\{\begin{array}{l}{-3x，x＜0}\\{x（x-2），x≥0}\end{array}\right.$；
当-2≤x＜0时，y=-3x∈（0，6]；
当0≤x≤2时，y=x（x-2）∈[-1，0]；
若输入值x∈[-2，2]，则输出值y的取值范围是[-1，6]．
故答案为：[-1，6]．
点评 本题考查了程序框图和分段函数的应用问题，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
5．如图，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$-$\overrightarrow{b}$=（ ）
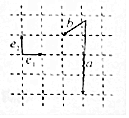
| A． | 3$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B． | -2$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$ | C． | $\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$ | D． | 3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ |
12．设由不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$表示的平面区域为Ω，P∈Ω，过点P作圆O：x2+y2=1的两条切线，切点分别为A、B，记∠APB=α，则当α最小时，cosα=（ ）
| A． | $\frac{\sqrt{95}}{10}$ | B． | $\frac{19}{20}$ | C． | $\frac{9}{10}$ | D． | $\frac{1}{2}$ |