题目内容
13.求不等式2cos($\frac{x}{2}$-$\frac{π}{4}$)>$\sqrt{3}$的解集.分析 画出y=cosx一个周期的图象,化简不等式后由余弦函数的图象和周期性,求出不等式的解集.
解答 解: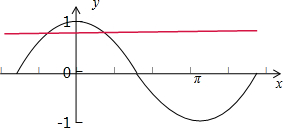 由2cos($\frac{x}{2}$-$\frac{π}{4}$)>$\sqrt{3}$得,
由2cos($\frac{x}{2}$-$\frac{π}{4}$)>$\sqrt{3}$得,
cos($\frac{x}{2}$-$\frac{π}{4}$)>$\frac{\sqrt{3}}{2}$,画出y=cosx一个周期的图象,
所以由图得,$-\frac{π}{6}+2kπ<\frac{x}{2}-\frac{π}{4}<\frac{π}{6}+2kπ,k∈Z$,
解得$\frac{π}{6}+4kπ<x<\frac{5π}{6}+4kπ,k∈Z$,
所以不等式的解集是$(\frac{π}{6}+4kπ,\frac{5π}{6}+4kπ),k∈Z$.
点评 本题考查利用余弦函数的图象和周期性求不等式的解集,考查数形结合思想.

练习册系列答案
相关题目
4.函数f(x)对任意实数x都满足条件f(x+2)f(x)=1,若f(2)=2,则f(2016)=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2016}$ | D. | 2016 |
1.命题“存在x0∈R,log2x0<0”的否定是( )
| A. | 对任意的x∈R,log2x<0 | B. | 对任意的x∈R,log2x≥0 | ||
| C. | 不存在x∈R,log2x≥0 | D. | 存在x0∈R,log2x0≥0 |
18.在正四面体ABCD中,E,F分别为棱AD,BC的中点,连接AF,CE,则异面直线AF与CE所成角的余弦值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
5.函数y=Asin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数的一个表达式为( )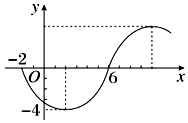

| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
2.某企业有甲乙两个分厂生产某种产品,按规定该产品的某项质量指标值落在[45,75)的为优质品,从两个分厂生产的产品中个随机抽取500件,测量这些产品的该项质量指标值,结果如表:
(1)根据以上统计数据完成下面2×2列联表,并回答是否有99%的把握认为:“两个分厂生产的产品的质量有差异”?
(2)求优质品率较高的分厂的500件产品质量指标值的样本平均数$\overline x$(同一组数据用该区间的中点值作代表)
(3)经计算,甲分厂的500件产品质量指标值的样本方差s2=142,乙分厂的500件差评质量指标值的样本方差s2=162,可认为优质品率较高的分厂的产品质量指标值X服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,由优质品率较高的厂的抽样数据,能够认为该分厂生产的产品的产品中,质量指标值不低于71.92的产品至少占全部产品的18%?
附注:
参考数据:$\sqrt{140}$≈11.92,$\sqrt{162}$≈12.73
参考公式:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(μ-2σ<x<μ+2σ)=0.9544,P(μ-3σ<x<μ+3σ)=0.9974.
| 分组 | [25,35) | [35,45) | [4,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 甲厂频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 乙厂频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
(2)求优质品率较高的分厂的500件产品质量指标值的样本平均数$\overline x$(同一组数据用该区间的中点值作代表)
(3)经计算,甲分厂的500件产品质量指标值的样本方差s2=142,乙分厂的500件差评质量指标值的样本方差s2=162,可认为优质品率较高的分厂的产品质量指标值X服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,由优质品率较高的厂的抽样数据,能够认为该分厂生产的产品的产品中,质量指标值不低于71.92的产品至少占全部产品的18%?
附注:
参考数据:$\sqrt{140}$≈11.92,$\sqrt{162}$≈12.73
参考公式:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(μ-2σ<x<μ+2σ)=0.9544,P(μ-3σ<x<μ+3σ)=0.9974.
| P(k2≥k) | 0.05 | 0.01 | 0.001 |
| h | 3.841 | 6.635 | 10.828 |
3.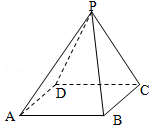 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )| A. | 4 | B. | 8 | C. | 12π | D. | 16π |