题目内容
18.在正四面体ABCD中,E,F分别为棱AD,BC的中点,连接AF,CE,则异面直线AF与CE所成角的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 画出立体图形,根据中点找平行线,把所求的异面直线角转化为一个三角形的内角来计算.
解答 解:由题意可得四面体A-BCD为正四面体,如图,连接BE,取BE的中点K,连接FK,则FK∥CE,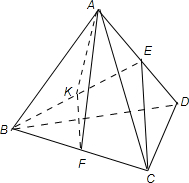
故∠AFK即为所求的异面直线角或者其补角.
设这个正四面体的棱长为2,在△AKF中,AF=$\sqrt{3}$=CE,KF=$\frac{1}{2}$CE=$\frac{\sqrt{3}}{2}$,KE=$\frac{1}{2}$BE=$\frac{\sqrt{3}}{2}$,
∴AK=$\sqrt{A{E}^{2}+K{E}^{2}}$=$\sqrt{{1}^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{7}}{2}$.
△AKF中,由余弦定理可得 cos∠AFK=$\frac{A{F}^{2}+F{K}^{2}-A{K}^{2}}{2AF•FK}$=$\frac{3+\frac{3}{4}-\frac{7}{4}}{2×\sqrt{3}×\frac{\sqrt{3}}{2}}$=$\frac{2}{3}$.
故选:A.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.函数$y=sin2x-\sqrt{3}cos2x$的图象可由函数$y=sin2x+\sqrt{3}cos2x$的图象至少向右平移( )个单位长度得到.
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{π}{6}$ |
9.运行如图所示的程序框图,则输出的结果S=( )


| A. | 1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$ | B. | $\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$ | C. | 1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$ | D. | $\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$ |
6.若圆x2+(y-1)2=3截直线y=kx-1所得的弦长为2,则斜率k的值是( )
| A. | $±\sqrt{2}$ | B. | $±\sqrt{3}$ | C. | ±1 | D. | ±2 |
3.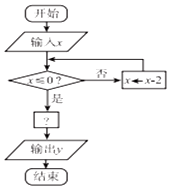 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
 如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )
如图是一个算法的程序框图,当输入的x的值为7时,输出的 y值恰好是-1,则“?”处应填的关系式可能是( )| A. | y=2x+1 | B. | y=3-x | C. | y=|x| | D. | y=log${\;}_{\frac{1}{3}}$x |
10.已知,0<β<α<$\frac{π}{4}$,cos(α-β)=$\frac{12}{13}$,且sin(α+β)=$\frac{4}{5}$,则sin2α的值为$\frac{63}{65}$.
8.已知正方体的表面积为24,则该正方体的体积为( )
| A. | 8 | B. | 27 | C. | 64 | D. | 125 |