题目内容
5.函数y=Asin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数的一个表达式为( )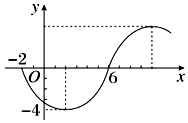
| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
分析 观察函数的图象可得A,由图可得周期T=16,代入周期公式T=$\frac{2π}{ω}$可求ω,再把函数图象上的最值点代入结合已知φ的范围可得φ的值,即可得解.
解答 解:由函数的图象可得最大值为4,且在一周期内先出现最小值,
所以A=-4,
观察图象可得函数的周期T=16,ω=$\frac{2π}{16}$=$\frac{π}{8}$,
又函数的图象过(2,-4)代入可得sin($\frac{π}{4}$+φ)=1,
∴φ+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{4}$,
∴函数的表达式y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$).
故选:A.
点评 本题主要考查了由三角函数的图象求解函数的解析式,其步骤一般是:由函数的最值求解A,(但要判断是先出现最大值或是最小值,从而判断A的正负号)由周期求解ω=2πT,由函数图象上的点(一般用最值点)代入求解φ,属于基础题.

练习册系列答案
相关题目
15.某地气象局预报说,明天本地降水概率为80%,你认为下面哪一个解释能表明气象局的观点.( )
| A. | 明天本地有80%的时间下雨,20%的时间不下雨 | |
| B. | 明天本地有80%的区域下雨,20%的区域不下雨 | |
| C. | 明天本地下雨的机会是80% | |
| D. | 气象局并没有对明天是否下雨作出有意义的预报 |