题目内容

3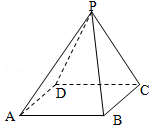．如图，在正四棱锥P-ABCD中，AB=2$\sqrt{3}$，侧面积为8$\sqrt{3}$，则它的体积为（　　）
A．4B．8C．12πD．16π

分析 作PO⊥平面ABCD，取BC中点E，连结OE，PE，求出PE=2，从而PO=1，由此能求出正四棱锥P-ABCD的体积．

解答 解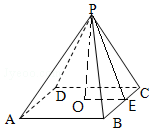：作PO⊥平面ABCD，取BC中点E，连结OE，PE，
∵正四棱锥P-ABCD中，AB=2$\sqrt{3}$，侧面积为8$\sqrt{3}$，
∴O是四边形ABCD的中点，E是BC的中点，PE⊥BC，
4×$\frac{1}{2}$BC×PE=8$\sqrt{3}$，解得PE=2，
∴PO=$\sqrt{P{E}^{2}-O{E}^{2}}$=$\sqrt{4-3}$=1，
∴正四棱锥P-ABCD的体积V=$\frac{1}{3}×{S}_{正方形ABCD}×PO$
=$\frac{1}{3}×2\sqrt{3}×2\sqrt{3}×1$=4．
故选：A．

点评 本题考查正四棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
13．求不等式2cos（$\frac{x}{2}$-$\frac{π}{4}$）＞$\sqrt{3}$的解集．
14．已知函数f（x）=|x-a|，若不等式f（x）≤3的解集为{|x|-1≤x≤5}．
（Ⅰ）求实数a的值：
（Ⅱ）若不等式f（3x）+f（x+3）≥m对一切实数x恒成立，求实数m的取值范围．
11．已知数列{an}是各项均不为零的等差数列，Sn为其前n项和，且${a_n}=\sqrt{{S_{2n-1}}}$（n∈N*）．若不等式$\frac{{λ{{（-1）}^n}}}{a_n}≤\frac{{n+2{{（-1）}^{n+1}}}}{n}$对任意n∈N*恒成立，则实数λ的取值范围是[-3，0]．
18．若椭圆C1：$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1（a1＞b1＞0）和椭圆C2：$\frac{{x}^{2}}{{{a}_{2}}^{2}}$+$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1（a2＞b2＞0）的焦点相同且a1＞a2．给出如下四个结论：
①椭圆C1与椭圆C2一定没有公共点        
②$\frac{{a}_{1}}{{a}_{2}}$＞$\frac{{b}_{1}}{{b}_{2}}$
③a12-a22=b12-b22
④a1-a2=b1-b2
其中所有正确结论的序号是（　　）
A．①②③B．①③④C．①②④D．②③④
8．已知正方体的表面积为24，则该正方体的体积为（　　）
A．8B．27C．64D．125
15．一种专门侵占内存的计算机病毒，开机时占据内存2KB，然后每3分钟自身复制一次，复制后所占内存是原来的2倍，若该病毒占据64MB内存（1MB=210KB），则开机后经过（　　）分钟．
A．45B．44C．46D．47
12．如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{18}$的值的一个程序框图，其中判断框内应填入的条件是（　　）
A．i＞9B．i＜9C．i＞18D．i＜18
13．已知集合A={1，t，2t}，B={1，t2}，若B⊆A，则实数t=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网