题目内容

在△ABC中，三个内角A、B、C的对边分别为a、b、c，若a=2，b=2
2
，∠C=15°，则内角A的值为（　　）
A、30°
B、60°
C、30°或150°
D、60°或120°
考点：余弦定理
专题：计算题,解三角形
分析：由余弦定理可得c2=8-4
3
，从而可得c=2
2-
3
，再次由余弦定理可得cosA的值为
3
2
，根据A的范围，即可求出A的值．
解答： 解：∵由余弦定理可得：c2=a2+b2-2abcosC=4+8-2×2×2
2
×cos15°
∴c2=8-4
3

∴c=2
2-
3

∴由余弦定理可得：cosA=
c2+b2-a2
2bc
=
8-4
3
+8-4
2×2
2
×2
2-
3
=
3-
3
2(
3
-1)
=
3
2

∵0＜A＜π
∴A=30°
故选：A．
点评：本题主要考察了余弦定理在解三角形中的应用，计算量比较大，属于中档题．
练习册系列答案
相关题目
设i为虚数单位，则复数z=
1+i
i
在复平面内对应的点所在的象限是（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
已知半径为2的圆C满足：①圆心在y轴的正半轴上；②它截x轴所得的弦长是2
3
，
（1）求圆C的方程；
（2）若直线l经过点P（2，-3），且与圆C相切，求直线l的方程．
已知集合U=R，A={x|1≤x≤4}，B={x|（x+2）（x-3）＜0}，C={x|m+1＜x＜2m-1}
（1）求A∪B，（CUA）∩B．
（2）若C⊆（A∪B），求m的取值范围．
已知动圆C过点M（0，
3
），且与圆N：x2+(y+
3
)2=16相内切．
（1）求圆心C的轨迹方程；
（2）设点A（1，0），点B在抛物线：y=x2+h（h∈R）上，以点B为切点作这条抛物线的切线l．使直线l与（1）中圆心C的轨迹相交于E，F两点，若线段AB的中点与线段EF的中点横坐标相等，求h的最小值．
在单调递减的等比数列{an}中，a1=
1
16
，若
5
4
a2是a1，a3的等差中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log2a1+log2a2+…+log2an，求数列{
1
bn
}的前项和Tn．
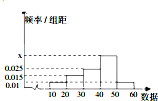 如图是一个样本数据的频率分布直方图，根据频率分布直方图，解答下列问题．
（Ⅰ）求图中x的值；
（Ⅱ）根据直方图，估计数据的众数和平均数（写出估计值、主要估计依据和方法）；
（Ⅲ）已知分布在第一组中有10个数据，求第三组和第四组数据个数之和．
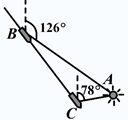如图，货轮在海上以35nmile/h的速度沿着方位角（从指北方向顺时针转到目标方向线的水平角）为148°的方向航行．为了确定船位，在B点观察灯塔A的方位角是126°，航行半小时后到达C点，观察灯塔A的方位角是78°．求货轮到达C点时与灯塔A的距离（精确到0.01nmile）．
设a，b都是正数，且满足
1
a
+
4
b
=1则使a+b＞c恒成立的实数c的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网