题目内容
若α=
,则计算1+sin(α-2π)•sin(π+α)-2cos2(-α)所得的结果为( )
| 7π |
| 6 |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:利用诱导公式化简表达式,求出α的正弦函数值,代入化简的表达式求解即可.
解答:
解:1+sin(α-2π)•sin(π+α)-2cos2(-α)
=1-sinα•sinα-2cos2α
=1-sinα•sinα-2+4sin2α
=-1+3sin2α
∵α=
,
∴sinα=sin
=-
.
∴1+sin(α-2π)•sin(π+α)-2cos2(-α)
=-1+3sin2α
=-1+3×
=-
.
故选:B.
=1-sinα•sinα-2cos2α
=1-sinα•sinα-2+4sin2α
=-1+3sin2α
∵α=
| 7π |
| 6 |
∴sinα=sin
| 7π |
| 6 |
| 1 |
| 2 |
∴1+sin(α-2π)•sin(π+α)-2cos2(-α)
=-1+3sin2α
=-1+3×
| 1 |
| 4 |
=-
| 1 |
| 4 |
故选:B.
点评:本题考查诱导公式的应用、三角函数值的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下程序运行后的输出结果为( )


| A、21 | B、13 | C、17 | D、25 |
下列说法正确的是( )
| A、对立事件也是互斥事件 |
| B、某事件发生的概率为1.1 |
| C、不能同时发生的两个事件是两个对立事件 |
| D、某事件发生的概率是随着实验次数的变化而变化的 |
曲线y=x3+1在x=0处的切线的斜率是( )
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、1 |
已知函数f(x)=
,则f(f(4))等于( )
|
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、2 |
已知函数f(x)=log2x,f(
)等于( )
| 1 |
| 4 |
| A、-1 | B、-2 | C、2 | D、3 |
下列各数中,最大的是( )
| A、32(8) |
| B、111(5) |
| C、101010(2) |
| D、54(6) |
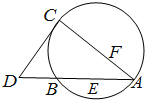 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为