题目内容
已知函数f(x)=
，则f（f（4））等于（ ）
|
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、2 |
考点：函数的值
专题：函数的性质及应用
分析：根据分段函数的表达式，直接代入计算即可．
解答：
解：由分段函数可知f（4）=log
4=-log24=-2，
∴f（f（4））=f（-2）=2-2=
，
故选：C．
| 1 |
| 2 |
∴f（f（4））=f（-2）=2-2=
| 1 |
| 4 |
故选：C．
点评：本题主要考查分段函数的应用，利用分段函数直接代入即可求解，注意分段函数的取值范围．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若对数函数y=logax在（0，+∞）上是减函数，那么（ ）
| A、0＜a＜1 | B、-1＜a＜0 |
| C、a=-1 | D、a＜-1 |
若抛物线x2=2py的焦点为F（0，2），则p的值为（ ）
| A、-2 | B、2 | C、-4 | D、4 |
若α=
，则计算1+sin（α-2π）•sin（π+α）-2cos2（-α）所得的结果为（ ）
| 7π |
| 6 |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
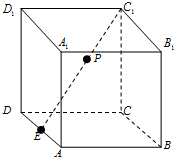如图，长方体ABCD-A1B1C1D1中，AB=3，BC=2，BB1=4，E为AD的中点，点P在线段C1E上，则点P到直线BB1的距离的最小值为（ ）| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
下面四个条件中，使a＞b成立的充分而不必要的条件是（ ）
| A、a2＞b2 |
| B、a3＞b3 |
| C、a＞b+1 |
| D、a＞b-1 |
已知命题p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列命题为真的是（ ）
| 1 |
| x |
| A、p∧q |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
已知实数a，b，则a+b＞0是a＞0且b＞0的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |