设a=0.5${\;}^{\frac{1}{2}}$.b=0.9${\;}^{\frac{1}{2}}$.c=log50.3.则a.b.c的大小关系是( )A．a＞c＞bB．c＞a＞bC．a＞b＞cD．b＞a＞c 题目和参考答案——青夏教育精英家教网—

题目内容

14．设a=0.5${\;}^{\frac{1}{2}}$，b=0.9${\;}^{\frac{1}{2}}$，c=log₅0.3，则a，b，c的大小关系是（　　）

A．

a＞c＞b

B．

c＞a＞b

C．

a＞b＞c

D．

b＞a＞c

分析利用指数函数、对数函数单调性直接求解．

解答解：∵0＜a=0.5${\;}^{\frac{1}{2}}$＜b=0.9${\;}^{\frac{1}{2}}$＜0.9⁰=1，
c=log₅0.3＜log₅1=0，
∴a，b，c的大小关系是b＞a＞c．
故选：D．

点评本题考查三个数的大小的求法，是基础题，解题时要认真审题，注意指数函数、对数函数单调性的合理运用．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

5．

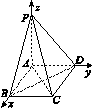如图，已知四边形ABCD为矩形，PA⊥平面ABCD，连接AC，BD，PB，PC，PD，则下列各组向量中，数量积不一定为零的是（　　）

A．

$\overrightarrow{PC}$与$\overrightarrow{BD}$

B．

$\overrightarrow{DA}$与$\overrightarrow{PB}$

C．

$\overrightarrow{PD}$与$\overrightarrow{AB}$

D．

$\overrightarrow{PA}$与$\overrightarrow{CD}$

2．在空间直角坐标系O-xyz中，有两点P（1，-2，3），M（2，0，4）则两点之间的距离为$\sqrt{6}$．

9．已知函数$f（x）=\frac{{-{3^x}+a}}{{{3^{x+1}}+b}}$．
（1）当a=b=1时，求满足f（x）=3^x的x的取值；
（2）若函数f（x）是定义在R上的奇函数存在t∈R，不等式f（t²-2t）＜f（2t²-k）有解，求k的取值范围．

19．对数式log_（2x-3）（x-1）中实数x的取值范围是（$\frac{3}{2}$，2）∪（2，+∞）．

6．计算：
（1）${（{-\frac{7}{8}}）^0}+\root{4}{{{{（{3-π}）}^4}}}$；
（2）（log₃2+log₉2）•（log₄3+log₈3）

3．化简、求值．
（Ⅰ）$\sqrt{{a^{\frac{1}{4}}}•\sqrt{a•\sqrt{a}}}$
（Ⅱ）log₂3•log₃5•log₅4．

4．下列关系中正确的是（　　）

	A．	（$\frac{1}{2}$）${\;}^{\frac{2}{3}}$＜2${\;}^{\frac{2}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$		B．	（$\frac{1}{2}$）${\;}^{\frac{2}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$＜2${\;}^{\frac{2}{3}}$
	C．	2${\;}^{\frac{2}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{2}{3}}$		D．	2${\;}^{\frac{2}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{2}{3}}$＜（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$

试题分类