题目内容
3．化简、求值．（Ⅰ）$\sqrt{{a^{\frac{1}{4}}}•\sqrt{a•\sqrt{a}}}$
（Ⅱ）log23•log35•log54．
分析 （1）根据指数幂的运算性质可得，
（2）根据对数的运算性质可得．
解答 解：（Ⅰ）$\sqrt{{a^{\frac{1}{4}}}•\sqrt{a•\sqrt{a}}}={（{a^{\frac{1}{4}}}{（a•{a^{\frac{1}{2}}}）^{\frac{1}{2}}}）^{\frac{1}{2}}}={a^{\frac{1}{2}}}=\sqrt{a}$；
（Ⅱ）${log_2}3•{log_3}5•{log_5}4=\frac{lg3}{lg2}•\frac{lg5}{lg3}•\frac{lg4}{lg5}=\frac{lg4}{lg2}=2$．
点评 本题考查了指数幂和对数的运算性质，属于基础题．
练习册系列答案
相关题目
13．
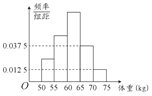为了了解我校今年报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则报考飞行员的学生人数是（ ）
为了了解我校今年报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则报考飞行员的学生人数是（ ）| A． | 50 | B． | 47 | C． | 48 | D． | 52 |
14．设a=0.5${\;}^{\frac{1}{2}}$，b=0.9${\;}^{\frac{1}{2}}$，c=log50.3，则a，b，c的大小关系是（ ）
| A． | a＞c＞b | B． | c＞a＞b | C． | a＞b＞c | D． | b＞a＞c |
11．设函数$f（x）=x-\frac{1}{x}$，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是 （ ）
| A． | m＜-1或0＜m＜1 | B． | 0＜m＜1 | C． | m＜-1 | D． | -1＜m＜0 |
15．直线y=kx+1-2k与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的位置关系为（ ）
| A． | 相交 | B． | 相切 | C． | 相离 | D． | 不确定 |
12．若$α∈（0，\frac{π}{2}）$，若$cos（α+\frac{π}{6}）=\frac{4}{5}$，则$sin（2α+\frac{π}{3}）$的值为（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{24}{25}$ | C． | $-\frac{24}{25}$ | D． | $-\frac{12}{25}$ |