题目内容
若tanα=3，则sin2α+sin2α的值等于（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：将所求的关系式的分母化为1后，将“弦”化“切”，得到原式=
，再将tanα=3代入计算即可得到答案．
| 2tanα+tan2α |
| tan2α+1 |
解答：
解：∵tanα=3，
∴sin2α+sin2α=
=
=
=
．
故选：D．
∴sin2α+sin2α=
| sin2α+sin2α |
| sin2α+cos2α |
| 2tanα+tan2α |
| tan2α+1 |
| 2×3+32 |
| 32+1 |
| 3 |
| 2 |
故选：D．
点评：本题考查同角三角函数基本关系的运用，分母化为1后，将“弦”化“切”是关键，属于中档题．
练习册系列答案
相关题目
下列四个命题：
（1）函数y=x+
的最小值是2；
（2）函数y=x2+
的最小值是2；
（3）函数y=
的最小值是2；
（4）函数y=2-3x-
（x＞0）的最大值是2-4
．
其中错误的命题个数是（ ）
（1）函数y=x+
| 1 |
| x |
（2）函数y=x2+
| 1 |
| x2 |
（3）函数y=
| x2+3 | ||
|
（4）函数y=2-3x-
| 4 |
| x |
| 3 |
其中错误的命题个数是（ ）
| A、2 | B、4 | C、3 | D、1 |
等比数列{an}中a2=4，a5=32则{an}的前6项和为（ ）
| A、128 | B、126 |
| C、140 | D、192 |
如图是一个算法步骤，根据要求解答问题．已知直线Ax+By+C=0不经过第一象限，且A，B，C均不为零，则有（ ）
| A、C＜0 | B、AB＜0 |
| C、ABC＜0 | D、AC＞0 |
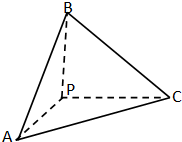三棱锥P-ABC中，三侧棱PA，PB，PC两两互相垂直，且三角形△PAB，△PAC，△PBC的面积依次为1，1，2，则此三棱锥 P-ABC外接球的表面积为（ ）| A、9π | B、12π |
| C、18π | D、36π |