题目内容
19.已知函数f(x)=2x3-3x2-12x+5.(Ⅰ)求曲线y=f(x)在点x=1处的切线方程;
(Ⅱ)求函数y=f(x)在[0,3]的最值.
分析 (I)利用切线的斜率是函数在切点处导数,求出切线斜率,再利用直线方程的点斜式求出切线方程.
(II)先求导函数,确定函数在闭区间[-2,3]上的极值点及端点的值,进而计算极值点及端点的函数值可确定函数的最值.
解答 解:(Ⅰ)将x=1代入函数解析式得y=-8,------------------------(2分)
函数f(x)=2x3-3x2-12x+5.
y'=6x2-6x-12=6(x-2)(x+1),所以y'|x=1=-12----------------------------------(4分)
由直线方程的点斜式得y+8=-12(x-1)
所以函数在x=1处的切线方程为12x+y-4=0----------------------------------(6分)
(Ⅱ)y'=6x2-6x-12=6(x-2)(x+1)=0,
解得x=2或x=-1------------------------(8分)
x∈[0,3]
由于f(0)=5,f(2)=-15,f(3)=-4,-------------------------------(10分)
∴ymax=5,ymin=-15------------------------------(12分)
点评 本题以函数为载体,考查函数导数的几何意义、利用导数求闭区间上函数的最值,解题的关键是利用导数工具.属于导数的基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设p:2x2-3x+1≤0,q:x2-(2a+1)x+a(a+1)≤0,若非p是非q的必要不充分条件,则实数a的取值范围是( )
| A. | (-∞,0)∪($\frac{1}{2}$,+∞) | B. | (-∞,0]∪[$\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | [0,$\frac{1}{2}$] |
7.我们知道:在平面内,点(x0,y0)到直线Ax+By+C=0的距离公式为d=$\frac{{|{A{x_0}+B{y_0}+C}|}}{{\sqrt{{A^2}+{B^2}}}}$,通过类比的方法,可求得:在空间中,点(2,4,1)到直线x+2y+2z+3=0的距离为( )
| A. | 3 | B. | 5 | C. | $\frac{{5\sqrt{21}}}{7}$ | D. | $3\sqrt{5}$ |
4.已知α,β是两个不重合的平面,m,n是两条不同的直线,则下列命题中正确的是( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥n,m∥α,则n∥α | ||
| C. | 若α⊥β,m⊥α,n⊥β,则m⊥n | D. | 若α⊥β,m⊥α,n∥β,则m∥n |
11.下列事件:
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
(2)在标准大气压下,水在90℃沸腾;
(3)射击运动员射击一次命中10环;
(4)同时掷两颗骰子,出现的点数之和不超过12,
其中是随机事件的有( )
(1)口袋里有伍角、壹角、壹元的硬币若干枚,随机地摸出一枚是壹角;
(2)在标准大气压下,水在90℃沸腾;
(3)射击运动员射击一次命中10环;
(4)同时掷两颗骰子,出现的点数之和不超过12,
其中是随机事件的有( )
| A. | (1) | B. | (1)(2) | C. | (1)(3) | D. | (2)(4) |
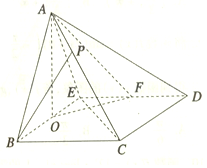 在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.
在四棱锥A-BCDE中,底面BCDE为菱形,侧面ABE为等边三角形,且侧面ABE⊥底面BCDE,O,F分别为BE,DE的中点,点P在AC上,且AP=$\frac{1}{3}$AC.