题目内容
14.现有n2(n≥4)个正数排列成一个n行n列的数表如下:$(\begin{array}{l}{{a}_{11}}&{{a}_{12}}&{…}&{{a}_{1n}}\\{{a}_{21}}&{{a}_{22}}&{…}&{{a}_{2n}}\\{…}&{…}&{…}&{…}\\{{a}_{n1}}&{{a}_{n2}}&{…}&{{a}_{nn}}\end{array})$
其中每一行的数都成等差数列,每一列的数都成等比数列且公比q都相等,若a26=1,a42=$\frac{1}{8}$,a44=$\frac{3}{16}$,则q的值为$\frac{1}{2}$.
分析 通过数列每一行的数成等差数列,求出a43,求得第四行的公差,可得a46,每一列的数成等比数列,由等比数列的通项公式,即可求公比q的值.
解答 解:因为每一行的数成等差数列,a42=$\frac{1}{8}$,a44=$\frac{3}{16}$,
∴a43=$\frac{1}{2}$(a42+a44)=$\frac{1}{2}$×($\frac{1}{8}$+$\frac{3}{16}$)=$\frac{5}{32}$,
即有第四行的公差为d=$\frac{5}{32}$-$\frac{1}{8}$=$\frac{1}{32}$,
可得a46=a42+4d=$\frac{1}{8}$+4×$\frac{1}{32}$=$\frac{1}{4}$,
每一列的数成等比数列a26=1,可得a46=a26•q2=q2=$\frac{1}{4}$,
因为正数排成n行n列方阵,
所以q>0,
解得q=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查等差数列和等比数列的通项公式和性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.若复数z满足|z|=3,且z的实部为1,则z的虚部为( )
| A. | 2$\sqrt{2}$i | B. | 2$\sqrt{2}$ | C. | ±2$\sqrt{2}$i | D. | ±2$\sqrt{2}$ |
3.命题“若a>b,则a-1>b-1”的逆否命题是( )
| A. | 若a<b,则a-1<b-1 | B. | 若a-1>b-1,则a>b | C. | 若a≤b,则a-1≤b-1 | D. | 若a-1≤b-1,则a≤b |
4.在△ABC中,已知点D为AB边的中点,点N在线段CD上,且$\overrightarrow{CN}$=2$\overrightarrow{ND}$,若$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{AC}$+λ$\overrightarrow{AB}$,则λ=( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
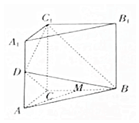 如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.
如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.