题目内容
已知不重合的平面α、β和不重合的直线m、n,给出下列命题:
①m∥n,n?α⇒m∥α;
②m∥n,n?α⇒m与α不相交;
③α∩β=m,n∥α,n∥β⇒n∥m;
④α∥β,m∥β,m?α⇒m∥α;
⑤m∥α,n∥β,m∥n⇒α∥β;
⑥m?α,n?β,α⊥β⇒m⊥n;
⑦m⊥α,n⊥β,α与β相交⇒m与n相交;
⑧m⊥n,n?β,m?β⇒m⊥β;
⑨α⊥β,a?α,b?β,b⊥a⇒b⊥α.
其中正确的个数为( )
①m∥n,n?α⇒m∥α;
②m∥n,n?α⇒m与α不相交;
③α∩β=m,n∥α,n∥β⇒n∥m;
④α∥β,m∥β,m?α⇒m∥α;
⑤m∥α,n∥β,m∥n⇒α∥β;
⑥m?α,n?β,α⊥β⇒m⊥n;
⑦m⊥α,n⊥β,α与β相交⇒m与n相交;
⑧m⊥n,n?β,m?β⇒m⊥β;
⑨α⊥β,a?α,b?β,b⊥a⇒b⊥α.
其中正确的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:在①中,m∥n,n?α⇒m∥α或m?α,故①错误;
②m∥n,n?α⇒m∥α或m?α,故m与α不相交,故②正确;
③α∩β=m,n∥α,n∥β,由直线与平面平行的性质得n∥m,故③正确;
④α∥β,m∥β,m?α,由直线与平面平行的性质得m∥α,故④正确;
⑤m∥α,n∥β,m∥n⇒α与β相交或平行,故⑤错误;
⑥m?α,n?β,α⊥β⇒m与n相交、平行或异面,故⑥错误;
⑦m⊥α,n⊥β,α与β相交⇒m与n相交或异面,故⑦错误;
⑧m⊥n,n?β,m?β⇒m与β相交或平行,故⑧错误;
⑨α⊥β,a?α,b?β,b⊥a⇒b与α相交、平行或b?α,故⑨错误.
故选:C.
②m∥n,n?α⇒m∥α或m?α,故m与α不相交,故②正确;
③α∩β=m,n∥α,n∥β,由直线与平面平行的性质得n∥m,故③正确;
④α∥β,m∥β,m?α,由直线与平面平行的性质得m∥α,故④正确;
⑤m∥α,n∥β,m∥n⇒α与β相交或平行,故⑤错误;
⑥m?α,n?β,α⊥β⇒m与n相交、平行或异面,故⑥错误;
⑦m⊥α,n⊥β,α与β相交⇒m与n相交或异面,故⑦错误;
⑧m⊥n,n?β,m?β⇒m与β相交或平行,故⑧错误;
⑨α⊥β,a?α,b?β,b⊥a⇒b与α相交、平行或b?α,故⑨错误.
故选:C.
点评:本题考查命题真假的判断,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
若集合M={0,1,2,3,4},N={x|x是偶数},则集合M∩N的子集个数为( )
| A、2 | B、4 | C、6 | D、8 |
已知函数f(x)定义域为[-1,4],则f(3x-1)的定义域为( )
| A、[4,19] | ||
B、[
| ||
C、[0,
| ||
D、[
|
已知椭圆
+
=1(a>b>0),F1,F2为左、右焦点,A1、A2、B1、B2分别是其左、右、上、下顶点,直线B1F2交直线B2A2于P点,若∠B1PA2为直角,则此椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分式方程
=
的解是( )
| 5 |
| x-2 |
| 3 |
| x |
| A、x=3 | ||
| B、x=-3 | ||
C、x=
| ||
D、x=-
|
已知直线m,平面α、β,下列命题中真命题是 ( )
| A、m∥α,α∥β⇒m∥β |
| B、m⊥α,α∥β⇒m⊥β |
| C、m∥α,α⊥β⇒m⊥β |
| D、m⊥α,α⊥β⇒m∥β |
已知集合p={x|(x-1)(x-3)≤0},Q={x||x|<2},则p∪Q等于( )
| A、[1,2) |
| B、[1,3] |
| C、(-2,3] |
| D、(-2,2) |
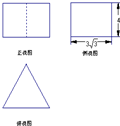 已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.
已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.