题目内容
7.若M为△ABC所在平面内的一点,且满足4$\overrightarrow{AM}$=2$\overrightarrow{AB}$+3$\overrightarrow{AC}$,直线BC与AM交于点D,则$\frac{|\overrightarrow{BD}|}{|\overrightarrow{BC}|}$=$\frac{3}{5}$.分析 由4$\overrightarrow{AM}$=2$\overrightarrow{AB}$+3$\overrightarrow{AC}$,得出$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)+$\frac{1}{4}$$\overrightarrow{AC}$,取BC的中点N,连接AN,取AE=$\frac{1}{4}$AC,得出$\overrightarrow{AM}$=$\overrightarrow{AN}$+$\overrightarrow{AE}$,画出图形结合图形求出$\frac{|\overrightarrow{BD}|}{|\overrightarrow{BC}|}$的值.
解答 解:△ABC中,
4$\overrightarrow{AM}$=2$\overrightarrow{AB}$+3$\overrightarrow{AC}$,
∴4$\overrightarrow{AM}$=2($\overrightarrow{AB}$+$\overrightarrow{AC}$)+$\overrightarrow{AC}$,
∴$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)+$\frac{1}{4}$$\overrightarrow{AC}$,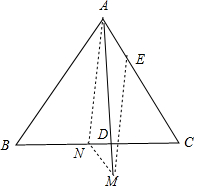
取BC的中点N,连接AN,取AE=$\frac{1}{4}$AC,
以$\overrightarrow{AN}$、$\overrightarrow{AE}$为邻边作平行四边形AEMN,连接AM,交BC于点D,
则$\overrightarrow{AM}$=$\overrightarrow{AN}$+$\overrightarrow{AE}$,如图所示;
∴MN=AE=$\frac{1}{4}$AC,
∴ND=$\frac{1}{4}$DC,
∴CD=$\frac{4}{5}$CN,
∴CD=$\frac{2}{5}$BC,
∴BD=$\frac{3}{5}$BC,
∴$\frac{|\overrightarrow{BD}|}{|\overrightarrow{BC}|}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查了平面向量的线性表示与运算问题,是中档题.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | (a-1)2>(b-1)2 | B. | lna>lnb | C. | a+b>1 | D. | $\sqrt{a}$<$\sqrt{b}$ |
| A. | $\frac{4n}{m}$ | B. | $\frac{2n}{m}$ | C. | $\frac{4m}{n}$ | D. | $\frac{2m}{n}$ |
| A. | $-\frac{16}{65}$ | B. | $\frac{56}{65}$ | C. | $\frac{56}{65}$或$\frac{16}{65}$ | D. | $\frac{56}{65}$或$-\frac{16}{65}$ |
 已知随机变量ξ服从正态分布N(1,σ2),如图所示.若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
已知随机变量ξ服从正态分布N(1,σ2),如图所示.若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8. 已知$f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象的一部分如图所示.
已知$f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的图象的一部分如图所示.