题目内容
如果（x2+x+1）（x+m）5展开式中所有项的系数是96，则展开式中x3项的系数是（ ）
| A、15 | B、20 | C、25 | D、45 |
考点：二项式系数的性质
专题：二项式定理
分析：根据题意，令x=1，求出m的值，再计算（x2+x+1）（x+1）5展开式中x3项的系数是多少．
解答：
解：根据题意，得；
当x=1时，（x2+x+1）（x+m）5展开式中所有项的系数为
3•（1+m）5=96，
解得m=1；
∴（x2+x+1）（x+1）5展开式中x3项的系数是
+
+
=5+10+10=25．
故选：C．
当x=1时，（x2+x+1）（x+m）5展开式中所有项的系数为
3•（1+m）5=96，
解得m=1；
∴（x2+x+1）（x+1）5展开式中x3项的系数是
| C | 1 5 |
| C | 2 5 |
| C | 3 5 |
故选：C．
点评：本题考查了二项式定理的应用问题，解题的关键是求出m的值，是基础题目．
练习册系列答案
相关题目
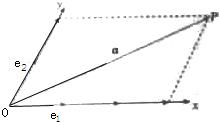如图，设Ox、Oy是平面内相交成60°角的两条数轴，