题目内容
已知Sn为数列{an}的前n项和,且有a1=1,Sn+1=an+1(n∈N*).
(Ⅰ) 求数列{an}的通项an;
(Ⅱ) 若bn=
,求数列{bn}的前n项和Tn;
(Ⅲ)是否存在最小正整数m,使得不等式
<m对任意正整数n恒成立,若存在,求出m的值;若不存在,说明理由.
(Ⅰ) 求数列{an}的通项an;
(Ⅱ) 若bn=
| n |
| 4an |
(Ⅲ)是否存在最小正整数m,使得不等式
| n |
 |
| k=1 |
| k+2 |
| Sk•(Tk+k+1) |
考点:数列与不等式的综合
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ) 当n=1时,求出a2=2,当n≥2时,求得an+1=2an,由此推导出{an}是首项为1,公比为2的等比数列,从而能求出an=2n-1.
(Ⅱ) 由bn=
=
=
,利用错位相减法能求出数列{bn}的前n项和Tn.
(Ⅲ)由
=2(
-
),能求出
=2(1-
)<2,由此推导出存在最小正整数m=2,使不等式
<m对任意正整数n恒成立.
(Ⅱ) 由bn=
| n |
| 4an |
| n |
| 4•2n-1 |
| n |
| 2n+1 |
(Ⅲ)由
| k+2 |
| Sk•(Tn+k+1) |
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
| n |
 |
| k=1 |
| k+2 |
| Sk•(Tk+k+1) |
| 1 |
| 2n+1-1 |
| n |
 |
| k=1 |
| k+2 |
| Sk•(Tk+k+1) |
解答:
解:(Ⅰ) 当n=1时,a2=S1+1=a1+1=2,…(1分)
当n≥2时,Sn+1=an+1,Sn-1+1=an,
两式相减得an+1=2an,…(2分)
又a2=2a1,∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1.…(4分)
(Ⅱ) 由(Ⅰ) 知an=2n-1,
bn=
=
=
,
∴Tn=
+
+
+…+
,
Tn=
+
+…+
+
,
两式相减得
Tn=
+
+
+…+
-
=
-
=
-
,
∴Tn=1-
.…(8分)
(Ⅲ)∵
=
=
=
=2(
-
),…(11分)
∴
=
2(
-
)
=2(1-
)<2,
若不等式
<m对任意正整数n恒成立,则m≥2,
∴存在最小正整数m=2,
使不等式
<m对任意正整数n恒成立.…(14分)
当n≥2时,Sn+1=an+1,Sn-1+1=an,
两式相减得an+1=2an,…(2分)
又a2=2a1,∴{an}是首项为1,公比为2的等比数列,
∴an=2n-1.…(4分)
(Ⅱ) 由(Ⅰ) 知an=2n-1,
bn=
| n |
| 4an |
| n |
| 4•2n-1 |
| n |
| 2n+1 |
∴Tn=
| 1 |
| 22 |
| 2 |
| 23 |
| 3 |
| 24 |
| n |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 23 |
| 2 |
| 24 |
| n-1 |
| 2n+1 |
| n |
| 2n+2 |
两式相减得
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n |
| 2n+2 |
=
| ||||
1-
|
| n |
| 2n+2 |
=
| 1 |
| 2 |
| n+2 |
| 2n+2 |
∴Tn=1-
| n+2 |
| 2n+1 |
(Ⅲ)∵
| k+2 |
| Sk•(Tn+k+1) |
| k+2 | ||
(2k-1)•(1-
|
=
| 1 | ||
(2k-1)•(1-
|
=
| 2k+1 |
| (2k-1)•(2k+1-1) |
=2(
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
∴
| n |
 |
| k=1 |
| k+2 |
| Sk•(Tk+k+1) |
| n |
 |
| k=1 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1-1 |
=2(1-
| 1 |
| 2n+1-1 |
若不等式
| n |
 |
| k=1 |
| k+2 |
| (Tk+k+1) |
∴存在最小正整数m=2,
使不等式
| n |
 |
| k=1 |
| k+2 |
| Sk•(Tk+k+1) |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查满足条件的实数是否存在的判断与求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
 如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离.
如图,我国某搜救舰艇以30(海里/小时)的速度在南海某区域搜索,在点A处测得基地P在南偏东60°,向北航行40分钟后到达点B,测得基地P在南偏东30°,并发现在北偏东60°的航向上有疑似马航飘浮物,搜救舰艇立即转向直线前往,再航行80分钟到达飘浮物C处,求此时P、C间的距离. 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}. 如图,已知△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.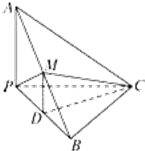 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.