题目内容
已知平面上定点O,A,B,向量
=
,
=
,且|
|=2,|
|=1,|
+
|=
,点C是平面上的动点,记
=
,若(
-2
)•(
-
)=0,给出以下命题:
①|
-
|=
;
②点C的轨迹是一个圆;
③|
|的最大值为
,最小值为
;
④|
|的最大值为
,最小值为
.
其中正确的有 (填上你认为正确的所有命题的序号)
| a |
| OA |
| b |
| OB |
| a |
| b |
| a |
| b |
| 7 |
| c |
| OC |
| a |
| c |
| b |
| c |
①|
| a |
| b |
| 3 |
②点C的轨迹是一个圆;
③|
| AC |
| ||
| 2 |
| ||
| 2 |
④|
| BC |
| ||
| 2 |
| ||
| 2 |
其中正确的有
考点:命题的真假判断与应用,平面向量数量积的运算
专题:平面向量及应用
分析:根据向量的数量积及模的性质,求出即
•
,和夹角θ=60°,再运用模的平方等于向量的平方,即可判断①,取OA的中点为A1,推出
⊥
,从而得到C的轨迹为圆,再由点A,B与圆的位置关系,求出AC,BC的最值,从而判断②③④.
| a |
| b |
| CA1 |
| CB |
解答:
解:∵|
|=2,|
|=1,|
+
|=
,
∴|
+
|2=|
|2+|
|2+2
•
=4+1+2
•
=7,
即
•
=1=2×1×cosθ,θ=60°,
①|
-
|=
=
=
,故①正确;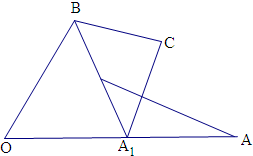
②若(
-2
)•(
-
)=0,取OA的中点为A1,
则(
-
)•(
-
)=0,即
⊥
,
故点C的轨迹为以A1B为直径的圆,即②正确;
③由②知C在以
为半径,A1B的中点为圆心的圆上运动,
则|
|的最大为
+
=
,
最小为
,故③正确;
④|
|的最大值为1,最小值为0,故④错.
故答案为:①②③.
| a |
| b |
| a |
| b |
| 7 |
∴|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即
| a |
| b |
①|
| a |
| b |
(
|
| 4+1-2×1 |
| 3 |

②若(
| a |
| c |
| b |
| c |
则(
| 1 |
| 2 |
| a |
| c |
| b |
| c |
| CA1 |
| CB |
故点C的轨迹为以A1B为直径的圆,即②正确;
③由②知C在以
| 1 |
| 2 |
则|
| AC |
1+
|
| 1 |
| 2 |
| ||
| 2 |
最小为
| ||
| 2 |
④|
| BC |
故答案为:①②③.
点评:本题考查平面向量的数量积的定义及运用,求模,求夹角,同时考查余弦定理和点与圆的位置关系,属于综合题.

练习册系列答案
相关题目
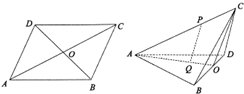 如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.
如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.