题目内容
已知函数f(x)=
sin2x-cos2x-
(x∈R).
(Ⅰ)求函数f(x)的最小值和最小正周期;
(Ⅱ)设△ABC的内角A、B、C的对边分别为a、b、c,且c=
,C=
,sinB-2sinA=0,求a、b.
| ||
| 2 |
| 1 |
| 2 |
(Ⅰ)求函数f(x)的最小值和最小正周期;
(Ⅱ)设△ABC的内角A、B、C的对边分别为a、b、c,且c=
| 3 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,余弦定理
专题:三角函数的图像与性质
分析:(Ⅰ)利用二倍角公式和两角和公式对函数解析式化简整理,继而根据三角函数的性质求得其最小值和最小正周期.
(Ⅱ)根据正弦定理和已知等式求得a和b的关系,进而利用余弦定理求得a,则b可求.
(Ⅱ)根据正弦定理和已知等式求得a和b的关系,进而利用余弦定理求得a,则b可求.
解答:
解:f(x)=
sin2x-cos2x-
=
sin2x-
-
=sin(2x-
)-1,
(Ⅰ)∴f(x)的最小值为-2,最小正周期T=
=π
(Ⅱ)∵sinB-2sinA=0,
∴b=2a,
由余弦定理得:c2=a2+b2-2abcosC,
即(
)2=a2+(2a)2-4a2cos
,
∴a=1或-1(舍去),
∴b=2.
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(Ⅰ)∴f(x)的最小值为-2,最小正周期T=
| 2π |
| 2 |
(Ⅱ)∵sinB-2sinA=0,
∴b=2a,
由余弦定理得:c2=a2+b2-2abcosC,
即(
| 3 |
| π |
| 3 |
∴a=1或-1(舍去),
∴b=2.
点评:本题主要考查了三角函数恒等变换的应用.要求学生对诸如二倍角公式,两角和公式三角函数性质和图象等知识能熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
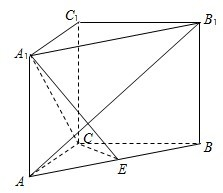 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.