题目内容
直线l:y=x+a(a≠0)和曲线C:y=x3-x2+1相切,求a的值及切点坐标.
考点:圆的切线方程
专题:直线与圆
分析:设直线l与曲线C相切于点P(x0,y0),根据导数的几何意义可得3x02-2x0=1,解得x0的值,可得a的值及切点坐标.
解答:
解:设直线l与曲线C相切于点P(x0,y0),则y=x3-x2+1的导数y′=3x2-2x.
由题意知直线l的斜率k=1,即3x02-2x0=1,解得x0=-
或x0=1.
因此,切点的坐标为(-
,
),或(1,1).
当切点为(-
,
)时,有
=-
+a,∴a=
;
当切点为(1,1)时,1=1+a,a=0(舍去).
所以a的值为
,切点坐标为(-
,
).
由题意知直线l的斜率k=1,即3x02-2x0=1,解得x0=-
| 1 |
| 3 |
因此,切点的坐标为(-
| 1 |
| 3 |
| 23 |
| 27 |
当切点为(-
| 1 |
| 3 |
| 23 |
| 27 |
| 23 |
| 27 |
| 1 |
| 3 |
| 32 |
| 27 |
当切点为(1,1)时,1=1+a,a=0(舍去).
所以a的值为
| 32 |
| 27 |
| 1 |
| 3 |
| 23 |
| 27 |
点评:本题主要考查导数的几何意义,属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
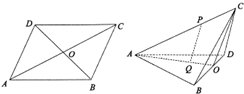 如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.
如图,ABCD为边长2的菱形,∠BAD=60°,对角线交于点O,沿BD将BCD折起,使二面角C-BD-A为120°,P为折起后AC上一点,且AP=2PC,Q为△ABD的中心.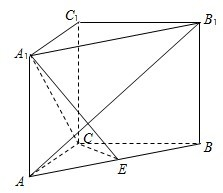 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.