题目内容
10.已知二次函数y=f(x)的图象过坐标原点,其导函数f′(x)=6x-2,数列{an}前n项和为Sn,点(n,Sn)(n∈N*)均在y=f(x)的图象上.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{3}{{{a_n}{a_{n+1}}}}$,Tn是数列{bn}的前n项和,求当${T_n}≥\frac{m}{20}$对所有n∈N*都成立m取值范围.
分析 (1)通过图象特征及导函数可知f(x)=3x2-2x,并代入点(n,Sn)(n∈N*)整理可知Sn=3n2-2n,进而与Sn-1=3(n-1)2-2(n-1)(n≥2)作差,计算即得结论;
(2)通过(1)裂项可知bn=$\frac{1}{2}$($\frac{1}{6n-5}$-$\frac{1}{6n+1}$),进而并项相加可知Tn=$\frac{3n}{1+6n}$,通过Tn=$\frac{1}{2}$(1-$\frac{1}{6n+1}$)随着n的增大而增大可知$\frac{3}{7}$≥$\frac{m}{20}$,进而计算可得结论.
解答 解:(1)依题意,f(x)=3x2-2x,
∵点(n,Sn)(n∈N*)均在y=f(x)的图象上,
∴Sn=f(n)=3n2-2n,
当n≥2时,Sn-1=3(n-1)2-2(n-1),
两式相减得:an=6n-5(n≥2),
又∵a1=S1=3-2=1满足上式,
∴数列{an}的通项公式an=6n-5;
(2)由(1)可知${b_n}=\frac{3}{{{a_n}{a_{n+1}}}}$=$\frac{3}{(6n-5)(6n+1)}$=$\frac{1}{2}$($\frac{1}{6n-5}$-$\frac{1}{6n+1}$),
∴数列{bn}的前n项和Tn=$\frac{1}{2}$(1-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{13}$+…+$\frac{1}{6n-5}$-$\frac{1}{6n+1}$)=$\frac{1}{2}$(1-$\frac{1}{6n+1}$)=$\frac{3n}{1+6n}$,
∵Tn=$\frac{1}{2}$(1-$\frac{1}{6n+1}$)随着n的增大而增大,
∴Tn≥T1=$\frac{3}{1+6}$=$\frac{3}{7}$,
又∵${T_n}≥\frac{m}{20}$对所有n∈N*都成立,
∴$\frac{3}{7}$≥$\frac{m}{20}$,解得:m≤$\frac{60}{7}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

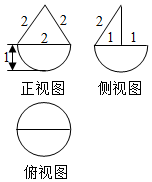
| A. | $\frac{4+\sqrt{3}}{3}$π | B. | $\frac{4+\sqrt{3}}{6}$π | C. | $\frac{2+\sqrt{3}}{3}$π | D. | $\frac{5π}{6}$ |

| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
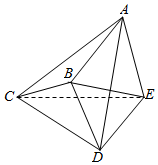 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.