题目内容
13．已知i是虚数单位，则复数z=$\frac{1+2i}{3-4i}$的虚部是（ ）| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | -$\frac{1}{5}$ | D． | $\frac{2}{5}$i |
分析 首先进行复数的乘法运算，得到复数的代数形式的标准形式，即可得到复数z=$\frac{1+2i}{3-4i}$的虚部．
解答 解：z=$\frac{1+2i}{3-4i}$=$\frac{（1+2i）（3+4i）}{（3-4i）（3+4i）}$=$\frac{-5+10i}{25}$=-$\frac{1}{5}$+$\frac{2i}{5}$，
故复数z=$\frac{1+2i}{3-4i}$的虚部是$\frac{2}{5}$，
故选：B．
点评 本题考查复数的代数形式的乘法运算和复数的基本概念，本题解题的关键是正确运算出结果，本题是一个基础题．
练习册系列答案
名校课堂系列答案
相关题目
4．阅读如图所示的程序框图，运行相应的程序，若判断框内是n≤6，则输出的S为（ ）
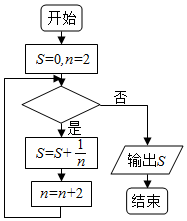
| A． | $\frac{3}{4}$ | B． | $\frac{25}{24}$ | C． | $\frac{11}{12}$ | D． | $\frac{5}{6}$ |
1．某几何体的三视图如图所示，则该几何体的体积为（ ）
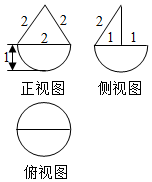
| A． | $\frac{4+\sqrt{3}}{3}$π | B． | $\frac{4+\sqrt{3}}{6}$π | C． | $\frac{2+\sqrt{3}}{3}$π | D． | $\frac{5π}{6}$ |
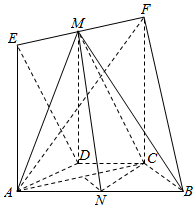如图，在几何体ABCDEF中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，FB=$\sqrt{10}$，M，N分别为EF，AB的中点．