题目内容
7.若集合$A=\{x|\frac{x+5}{x-2}<0\}$,B={x|-4<x<3},则集合A∩B为( )| A. | {x|-5<x<3} | B. | {x|-4<x<2} | C. | {x|-4<x<5} | D. | {x|-2<x<3} |
分析 求出A中不等式的解集确定出A,找出A与B的交集即可.
解答 解:由A中不等式变形得:(x+5)(x-2)<0,
解得:-5<x<2,即A={x|-5<x<2},
∵B={x|-4<x<3},
∴A∩B={x|-4<x<2},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
12.阅读如图所示的程序框图,运行相应的程序,输出的结果s=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
19.函数f(x)=sin2x和函数g(x)的部分图象如图所示,则函数g(x)的解析式可以是( )

| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
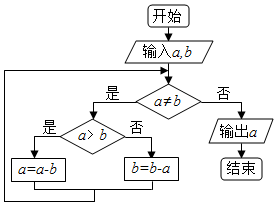 上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )
上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )