题目内容
19.已知数列{an}满足an=(n2+2n)sin$\frac{(2n-1)π}{2}$,则{an}的前100项的和为( )| A. | -2016 | B. | -5150 | C. | -5050 | D. | -2015 |
分析 由已知得an=(-1)n+1n2+2n,由此能求出{an}的前100项的和.
解答 解:∵an=(n2+2n)sin$\frac{(2n-1)π}{2}$,∴an=(-1)n+1n2+2n,
∴{an}的前100项的和:
Sn=(a1+a3+…+a99)-(a2+a4+…+a100)
=(12+2×1+32+2×3+52+2×5+…+992+2×99)-(22+2×2+42+2×4+62+2×6+…+1002+2×100)
=2(1+3+5+…+99)-2(2+4+6+8+…+100)+(12-22+32-42+52-62+…+992-1002)
=2×(-1)×50-(1+2+3+4+5+6+…+99+100)
=-100-5050
=-5150.
故选:B.
点评 本题考查数列的前100项和的求法,是中档题,解题时要认真审题,注意正弦函数的性质和分组求和法的合理运用.

练习册系列答案
相关题目
10.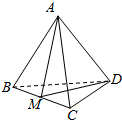 如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
 如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
7.如图是一个几何体的三视图.则该几何体的体积为( )


| A. | 6π | B. | 8π | C. | 12π | D. | 24π |
4.若全集U=R,集合A={x|0<x<2},B={x|x-1>0},则A∩∁UB=( )
| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
11.方程x2+y2-2kx+(4k+10)y+20k+25=0(k∈R)表示的圆中,任意两个圆的位置关系是( )
| A. | 一定外切 | B. | 一定内切 | ||
| C. | 一定不相交 | D. | 不能确定,与k的值有关 |
1.设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|1<x<4},则∁u(A∪B)=( )
| A. | {0,1,2,3} | B. | {5} | C. | {1,2,4} | D. | {0,4,5} |