题目内容
10．
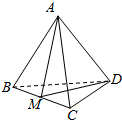如图所示的正四面体A-BCD中，截面ADM将其分成体积相等的两部分，则AB与截面ADM所成角为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 无法确定 |
分析 由已知M是BC的中点，从而AM⊥BC，DE⊥BC，进而BC⊥平面AMD，∠BAM是直线AB与截面ADM所成角，由此能求出AB与截面ADM所成角的大小．
解答 解：∵如图所示的正四面体A-BCD中，截面ADM将其分成体积相等的两部分，
∴M是BC的中点，
∵AB=AC=BD=DC，∴AM⊥BC，DE⊥BC，
∵AM∩DM=M，∴BC⊥平面AMD，
∴∠BAM是直线AB与截面ADM所成角，
∵BM=$\frac{1}{2}AB$，BM⊥AM，
∴sin∠BAM=$\frac{BM}{AB}$=$\frac{1}{2}$，∴∠BAM=30°．
∴AB与截面ADM所成角为30°．
故选：A．
点评 本题考查线面角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
1．已知数列{an}满足an+1=2an（n∈N*），其前n项和为Sn，则$\frac{S_5}{a_5}$=（ ）
| A． | $\frac{15}{16}$ | B． | $\frac{31}{16}$ | C． | $\frac{15}{32}$ | D． | $\frac{31}{32}$ |
19．已知数列{an}满足an=（n2+2n）sin$\frac{（2n-1）π}{2}$，则{an}的前100项的和为（ ）
| A． | -2016 | B． | -5150 | C． | -5050 | D． | -2015 |
13．设定义在R上的奇函数y=f（x），满足对任意t∈R都有$f（{\frac{1}{2}-t}）=f（{\frac{1}{2}+t}）$，且x∈[0，$\frac{1}{2}$]时，f（x）=-x2，则f（3）+f（-$\frac{3}{2}$）的值等于（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{1}{3}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{1}{5}$ |