题目内容
12.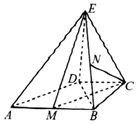 如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.
如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.(Ⅰ)若M是AB的中点,求证:平面CEM⊥平面BDE;
(Ⅱ)若N为BE的中点,求证:CN∥平面ADE.
分析 (Ⅰ)由ED⊥平面ABCD,可得ED⊥AD,ED⊥BD,由AE=BE,利用三角形全等可得AD=BD.再由M是AB的中点,得DM⊥AB,结合已知可得四边形BCDM是正方形,得BD⊥CM.由线面垂直的判定可得CM⊥平面BDE,从而得到平面CEM⊥平面BDE;
(Ⅱ)由(Ⅰ)知,AB=2CD,取AE中点G,连接NG,DG,由三角形中位线定理结合已知可得NG=$\frac{1}{2}$AB,再由AB∥CD,且AB=2CD,可得四边形CDGN为平行四边形,由线面平行的判定可得.
解答 证明:(Ⅰ)∵ED⊥平面ABCD,∴ED⊥AD,ED⊥BD,
∵AE=BE,∴△ADE≌△BDE,则AD=BD.
连接DM,则DM⊥AB,
∵AB∥CD,∠BCD=90°,BC=CD,
∴四边形BCDM是正方形,则BD⊥CM.
又DE⊥CM,∴CM⊥平面BDE,
∵CM?平面CEM,∴平面CEM⊥平面BDE;
(Ⅱ)由(Ⅰ)知,AB=2CD,取AE中点G,连接NG,DG,
在△EBA中,∵N为BE的中点,∴NG∥AB且NG=$\frac{1}{2}$AB,
又AB∥CD,且AB=2CD,∴NG∥CD,且NG=CD,
又四边形CDGN为平行四边形,∴CN∥DG.
又∵CN?平面ADE,DG?平面ADE,
∴CN∥平面ADE.
点评 本题考查直线与平面平行,平面与平面垂直的判定,考查空间想象能力和思维能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知i是虚数单位,复数$z=\frac{3+i}{1+i}$对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
3.若复数z满足(1+i)z=2-i,则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.若集合A={x|x≥0},且A∩B=B,则集合B可能是( )
| A. | {x|x≥2} | B. | {x|x≤1} | C. | {x|x≥-1} | D. | R |
4.i为虚数单位,复数$z=\frac{i-1}{i+1}$的虚部为( )
| A. | 1 | B. | 0 | C. | i | D. | 以上都不对 |
2.已知全集U为实数集,集合A={x|x2-2x-3<0},B={x|y=ln(1-x)},则A∩(∁UB)为( )
| A. | {x|1≤x<3} | B. | {x|x<3} | C. | {x|x≤-1} | D. | {x|-1<x<1} |
 某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$.
某程序框图如图所示,若运行该程序后输出S为$\frac{5}{6}$.