题目内容
1.已知点G是△ABC的重心,内角A、B、C所对的边长分别为a、b、c,且$\frac{a}{5}\overrightarrow{GA}+\frac{b}{7}\overrightarrow{GB}+\frac{c}{8}\overrightarrow{GC}=\overrightarrow 0$,则角B的大小是$\frac{π}{3}$.分析 点G是△ABC的重心,可得:$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$,由题意$\frac{a}{5}\overrightarrow{GA}+\frac{b}{7}\overrightarrow{GB}+\frac{c}{8}\overrightarrow{GC}=\overrightarrow 0$,可得a=5,b=7,c=8,根据余弦定理可得角B的大小.
解答 解:由题意:点G是△ABC的重心,可得:$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow 0$,
∵$\frac{a}{5}\overrightarrow{GA}+\frac{b}{7}\overrightarrow{GB}+\frac{c}{8}\overrightarrow{GC}=\overrightarrow 0$,
∴可得a=5,b=7,c=8,
由余弦定理可得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{25+64-49}{80}=\frac{1}{2}$,
∵0<B<π,
∴B=$\frac{π}{3}$.
故答案为$\frac{π}{3}$
点评 本题考查重心的性质,是基础题,解题时要认真审题.

练习册系列答案
相关题目
9.设当x=θ时,函数y=3sinx-cosx取得最大值,则sinθ=( )
| A. | $-\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $-\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
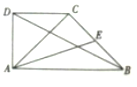 如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.
如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.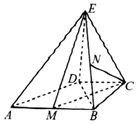 如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.
如图,在直角梯形ABCD中,AB∥CD,AB=2CD,∠BCD=90.,BC=CD,AE=BE,ED⊥平面ABCD.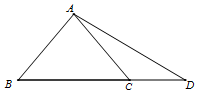 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.