题目内容
19.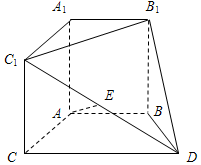 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.(Ⅰ)求证:AE∥平面BB1D;
(Ⅱ)当AE与平面ABCD所成角的正切值为$\frac{1}{2}$时,求该几何体的体积.
分析 (Ⅰ)取CD中点G,连接EG、AG,则EG∥CC1∥BB1,可得EG∥平面BDB1,再由AB∥CD,AB=$\frac{1}{2}CD$,可得四边形ABDG为平行四边形,则AG∥BD,从而AG∥平面BDB1,由面面平行的判定可得平面AEG∥平面BDB1,
则AE∥平面BB1D;
(Ⅱ)由已知求得直三棱柱的高,然后由直三棱柱的体积与三棱锥B1-BCD的体积作和求得几何体的体积.
解答 (Ⅰ)证明:取CD中点G,连接EG、AG,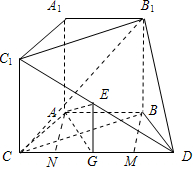
则EG∥CC1∥BB1,∴EG∥平面BDB1,
∵AB∥CD,AB=$\frac{1}{2}CD$,∴四边形ABDG为平行四边形,则AG∥BD.
∴AG∥平面BDB1,
又AG∩GE=G,∴平面AEG∥平面BDB1,
则AE∥平面BB1D;
(Ⅱ)解:在平面ABCD内,过B作BM⊥CD,垂足为M,
在Rt△BMD中,∵BD=2,∠BDC=60°,∴DM=1,BM=$\sqrt{3}$.
${S}_{△ABC}=\frac{1}{2}×AB×BM=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
${S}_{△BCD}=\frac{1}{2}×CD×BM=\frac{1}{2}×4×\sqrt{3}=2\sqrt{3}$.
∵AE与平面ABCD所成角的正切值为$\frac{1}{2}$,∴tan∠EAG=$\frac{1}{2}$,
又AG=BD=2,∴EG=1,则CC1=2.
∴几何体的体积V=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}+{V}_{{B}_{1}-BCD}$=$\sqrt{3}×2+\frac{1}{3}×2\sqrt{3}×2=\frac{10\sqrt{3}}{3}$.
点评 本题考查面面平行的判定及性质,考查空间想象能力和思维能力,训练了利用等体积法求多面体的体积,属中档题.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | $\sqrt{2}+1$ | B. | $2({\sqrt{2}+1})$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |

| A. | 20、32、77 | B. | 77、20、32 | C. | 32、20、77 | D. | 77、32、20 |
| A. | λ≥$\frac{1}{9}$ | B. | λ≥2 | C. | λ≥-$\frac{8}{9}$ | D. | λ≥-13 |