题目内容
17.设数列{an}的各项均为不等的正整数,其前n项和为Sn,我们成满足条件“对任意的m,n∈N*,均有(n-m)Sm+n=(m+n)(Sn-Sm)”的数列{an}为“好”数列.(1)试判断数列{an},{bn}是否为“好”数列,其中${a_n}=2n-1,{b_n}={2^{n-1}},n∈{N^*}$,并给出证明.
(2)已知数列{cn}为“好”数列.
①c2016=2017,求数列的通项公式;
②若c1=p,且对任意的给定正整数p,s(s>1),有c1,cs,ct成等比数列,求证:t≥s2.
分析 (1)由an=2n-1,运用等差数列的求和公式,可得Sn;检验(n-m)Sm+n=(m+n)(Sn-Sm)是否恒成立,即可判断;对bn=2n-1,取n=2,m=1,代入(n-m)Sm+n=(m+n)(Sn-Sm),计算是否成立,即可判断;
(2)对任意的m,n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm),令m=1,则(n-1)Sn+1=(n+1)(Sn-a1).化为ncn+1=Sn+1+Sn-(n+1)c1,n≥2时,(n-1)cn=Sn+Sn-1-nc1,化为(n-1)cn+1-ncn=-c1,利用递推关系可得:cn+1+cn-1=2cn.因此数列{cn}是等差数列.由c2016=2017=c1+2015d,即2017-c1=2015d,由于数列{cn}的各项均为不等正整数,可得d=1.即可得出①数列的通项公式;
②若c1=p,则cn=dn+p-d.由c1,cs,ct成等比数列,运用等比数列的中项性质,结合等差数列的通项公式,化简整理,求得t的表达式,分析整理由不等式的性质,即可得证.
解答 解:(1)由an=2n-1,可得Sn=$\frac{n(1+2n-1)}{2}$=n2,
从而(n-m)Sn+m=(n-m)(n+m)2,(n+m)(Sn-Sm)=(n+m)(n2-m2)=(n-m)(n+m)2,
故对任意的m,n∈N*,均有(n-m)Sm+n=(m+n)(Sn-Sm),则数列{an}为“好”数列;
若bn=2n-1,取n=2,m=1,可得(n-m)Sn+m=S3=1+2+4=7,(m+n)(Sn-Sm)=3×(1+2-1)=6,
此时(n-m)Sm+n≠(m+n)(Sn-Sm),即有数列{cn}不为“好”数列;
(2)①∵对任意的m,n∈N*,均有(n-m)Sn+m=(n+m)(Sn-Sm),
令m=1,则(n-1)Sn+1=(n+1)(Sn-a1).化为ncn+1=Sn+1+Sn-(n+1)c1,
n≥2时,(n-1)cn=Sn+Sn-1-nc1,
∴ncn+1-(n-1)cn=cn+1+cn-c1,
∴(n-1)cn+1-ncn=-c1,
(n-2)cn-(n-1)cn-1=-c1,
∴(n-1)(cn+1+cn-1)=2(n-1)cn,
∴cn+1+cn-1=2cn.
∴数列{cn}是等差数列.
∵c2016=2017=c1+2015d,即2017-c1=2015d,
∵数列{cn}的各项均为不等的正整数,∴d=1.
则c1=2,∴cn=2+(n-1)=1+n;
②证明:若c1=p,则cn=dn+p-d.
由c1,cs,ct成等比数列,
可得cs2=c1ct,
即为(ds+p-d)2=p(dt+p-d),
化简可得p(t+1-2s)=d(s-1)2,
即d=$\frac{t+1-2s}{(s-1)^{2}}$•p,
对任意的给定正整数p,要使d为正整数,
必须使$\frac{t+1-2s}{(s-1)^{2}}$为正整数,
不妨设k=$\frac{t+1-2s}{(s-1)^{2}}$,s>1且为给定正整数,
可得t=k(s-1)2+2s-1≥(s-1)2+2s-1=s2,
即有t≥s2.
点评 本题考查新定义的理解和运用,考查等差数列和等比数列的通项公式和求和公式的运用,以及化简整理的运算能力,推理性强,具有一定的综合性,属于难题.

| A. | $\sqrt{2}+1$ | B. | $2({\sqrt{2}+1})$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
| A. | λ≥$\frac{1}{9}$ | B. | λ≥2 | C. | λ≥-$\frac{8}{9}$ | D. | λ≥-13 |
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>a>c |
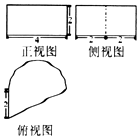 已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为( )| A. | 4π+8 | B. | 4π+12 | C. | 8π+8 | D. | 8π+12 |
| A. | 23 | B. | 24 | C. | $\frac{{24\sqrt{17}}}{17}-1$ | D. | $\frac{{24\sqrt{17}}}{17}$ |