Question

14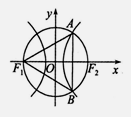．F₁、F₂分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，以坐标原点O为圆心，|OF₂|为半径的圆与该双曲线右支交于A、B两点，若△F₁AB是等边三角形，则双曲线的离心率为（　　）

• A． $\sqrt{3}$
• B． 2
• C． $\sqrt{3}$-1
• D． 1+$\sqrt{3}$

Answer 1

分析 连结AF₁，根据圆的直径的性质和等边三角形的性质，证出△F₁AF₂是含有30°角的直角三角形，由此得到|F₁A|=c且|F₂A|=$\sqrt{3}$c．再利用双曲线的定义，得到2a=|F₂A|-|F₁A|=（ $\sqrt{3}$-1）c，即可算出该双曲线的离心率．

解答 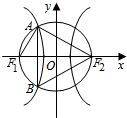解：连结AF₁，
∵F₁F₂是圆O的直径，
∴∠F₁AF₂=90°，即F₁A⊥AF₂，
又∵△F₂AB是等边三角形，F₁F₂⊥AB，
∴∠AF₂F₁=$\frac{1}{2}$∠AF₂B=30°，
因此，Rt△F₁AF₂中，|F₁F₂|=2c，|F₁A|=$\frac{1}{2}$|F₁F₂|=c，
|F₂A|=$\frac{\sqrt{3}}{2}$|F₁F₂|=$\sqrt{3}$c．
根据双曲线的定义，得2a=|F₂A|-|F₁A|=（$\sqrt{3}$-1）c，
解得c=（$\sqrt{3}$+1）a，
∴双曲线的离心率为e=$\frac{c}{a}$=$\sqrt{3}$+1．
故选：D．

点评 本题给出以双曲线焦距F₁F₂为直径的圆交双曲线于A、B两点，在△F₂AB是等边三角形的情况下求双曲线的离心率．着重考查了双曲线的定义、标准方程与简单几何性质等知识，属于中档题．