题目内容
2. 如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是( )
如图,圆O内有一个内接三角形ABC,且直径AB=2,∠ABC=45°,在圆O内随机撒一粒黄豆,则它落在三角形ABC内(阴影部分)的概率是( )| A. | $\frac{1}{2π}$ | B. | $\frac{\sqrt{2}}{2π}$ | C. | $\frac{\sqrt{3}}{2π}$ | D. | $\frac{1}{π}$ |
分析 根据题意,计算圆O的面积S圆和△ABC的面积S△ABC,求它们的面积比即可.
解答 解:圆O的直径AB=2,半径为1,
所以圆的面积为S圆=π•12=π;
△ABC的面积为S△ABC=$\frac{1}{2}$•2•1=1,
在圆O内随机撒一粒黄豆,它落在△ABC内(阴影部分)的概率是
P=$\frac{{S}_{△ABC}}{{S}_{圆}}$=$\frac{1}{π}$.
故选:D.
点评 本题考查了几何概型的概率计算问题,是基础题.

练习册系列答案
相关题目
12.为了得到函数$y=2sin({\frac{x}{3}+\frac{π}{4}})$,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |
13.若x、y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y-2≤0}\\{2x-y-2≥0}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
10.某班级有一个7人的小组,现选出其中3人调整座位且3人座位都有变动,其余4人座位不变,则不同的调整方案有( )
| A. | 35种 | B. | 70种 | C. | 210种 | D. | 105种 |
17.已知cosα=-$\frac{3}{5}$,α是第三象限的角,则sinα=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{3}$ |
14.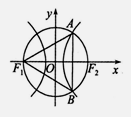 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
11.设数列{an}满足a1=1,an+1•an=2n(n∈N*),若Sn为数列前n项和,则S2016=( )
| A. | 22016-1 | B. | 3•21008-3 | C. | 22009-3 | D. | 22010-3 |
 如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图:
如图,甲、乙两名篮球运动员的季后赛10场得分可用茎叶图表示如图: