题目内容
4.已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.(1)求数列{an}的通项公式;
(2)令${b_n}={a_n}•{3^n}$(n∈N*),求数列{bn}的前n项和.
分析 (1)利用等差数列的通项公式即可得出.
(2)利用错位相减法与等比数列的求和公式即可的.
解答 解:(1)设等差数列{an}的公差为d,∵a1=2,a1+a2+a3=12.
∴3×2+3d=12,解得d=2.
∴an=2+2(n-1)=2n.
(2)${b_n}={a_n}•{3^n}$=2n•3n,
∴数列{bn}的前n项和Tn=2(3+2×32+3×33+…+n•3n).
3Tn=2[32+2×33+…+(n-1)•3n+n•3n+1],
∴-2Tn=2(3+32+…+3n)-2×n•3n+1=2×$\frac{3({3}^{n}-1)}{3-1}$-2×n•3n+1,
化为:Tn=$\frac{(2n-1)•{3}^{n+1}+3}{2}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、错位相减法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
12.为了得到函数$y=2sin({\frac{x}{3}+\frac{π}{4}})$,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |
19.已知不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,则实数m的取值范围为( )
| A. | (-∞,-5)∪(1,+∞) | B. | (1,19) | C. | [1,19) | D. | (19,+∞) |
9.阅读下列程序:

若输入5,则程序运行的结果为( )

若输入5,则程序运行的结果为( )
| A. | 1 | B. | 10 | C. | 25 | D. | 26 |
13.若x、y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y-2≤0}\\{2x-y-2≥0}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
14.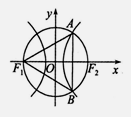 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为( )
的最小值为( )