题目内容
5.已知A(0,1),B、C为椭圆x2+my2=m(m>1)上的三个不同点,AB⊥AC.(Ⅰ)当椭圆长轴长为4时,求椭圆的离心率e;
(Ⅱ)求△ABC面积的最大值f(m).
分析 (Ⅰ)化椭圆方程化为标准形式,结合题意可得$2\sqrt{m}=4$,求得m值,则椭圆的离心率可求;
(Ⅱ)不妨设直线AB为y=kx+1(k>0).联立直线方程与椭圆方程,求得B,C的坐标,得到|AB|,|AC|,写出△ABC的面积,换元后分类讨论求最值.
解答 解:(Ⅰ)椭圆方程化为$\frac{{x}^{2}}{m}+{y}^{2}=1$.
由题意知:$2\sqrt{m}=4$,得m=4.
∴a=2,$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{3}$.
∴e=$\frac{\sqrt{3}}{2}$;
(Ⅱ)不妨设直线AB为y=kx+1(k>0).
联立$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}+m{y}^{2}=m}\end{array}\right.$,得(1+mk2)x2+2mkx=0.
解得:x=0或x=$\frac{-2mk}{1+m{k}^{2}}$.
∴|AB|=$\frac{2mk}{1+m{k}^{2}}\sqrt{1+{k}^{2}}$,同理可得:|AC|=$\frac{\frac{2m}{k}}{1+\frac{m}{{k}^{2}}}\sqrt{1+\frac{1}{{k}^{2}}}$.
∴${S}_{△ABC}=\frac{2{m}^{2}•\sqrt{2+{k}^{2}+\frac{1}{{k}^{2}}}}{1+{m}^{2}+m({k}^{2}+\frac{1}{{k}^{2}})}$,令$\sqrt{2+{k}^{2}+\frac{1}{{k}^{2}}}=t$,t≥2.
∴${S}_{△ABC}=\frac{2{m}^{2}t}{1+{m}^{2}+m({t}^{2}-2)}=\frac{2{m}^{2}}{mt+\frac{(m-1)^{2}}{t}}$.
①当$\frac{m-1}{\sqrt{m}}≤2$,即$1<m≤3+2\sqrt{2}$时,$[mt+\frac{(m-1)^{2}}{t}]_{min}=2m+\frac{(m-1)^{2}}{2}$,
∴f(m)=$\frac{4{m}^{2}}{(m+1)^{2}}$;
②当$\frac{m-1}{\sqrt{m}}$>2,即m>$3+2\sqrt{2}$时,$[mt+\frac{(m-1)^{2}}{t}]_{min}=2\sqrt{m(m-1)^{2}}$.
∴$f(m)=\frac{{m}^{2}}{\sqrt{m(m-1)^{2}}}$.
故f(m)=$\left\{\begin{array}{l}{\frac{4{m}^{2}}{(m+1)^{2}},1<m≤3+2\sqrt{2}}\\{\frac{{m}^{2}}{\sqrt{m(m-1)^{2}}},m>3+2\sqrt{2}}\end{array}\right.$.
点评 本题考查椭圆的简单性质,考查直线与圆锥曲线位置关系的应用,训练了利用换元法求函数的最值,属难题.

| A. | -4 | B. | 2 | C. | $\frac{8}{3}$ | D. | 4 |
| A. | 35种 | B. | 70种 | C. | 210种 | D. | 105种 |
| A. | -$\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{3}$ |
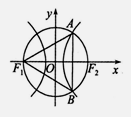 F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,以坐标原点O为圆心,|OF2|为半径的圆与该双曲线右支交于A、B两点,若△F1AB是等边三角形,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$-1 | D. | 1+$\sqrt{3}$ |
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.