题目内容
9．
如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，△PAB是等边三角形，AC⊥BC，且AC=BC=2，O、D分别是AB，PB的中点．（1）求证：PA∥平面COD；
（2）求三棱锥P-ABC的体积．
分析 （1）由O、D分别是AB，PB的中点，得OD∥AP，即可得PA∥平面COD．
（2）连接OP，得OP⊥面ABC，且OP=$\frac{\sqrt{3}}{2}×2\sqrt{2}=\sqrt{6}$．即可得三棱锥P-ABC的体积V=$\frac{1}{3}{s}_{ABC}×OP=\frac{1}{3}×\frac{1}{2}×{2}^{2}×\sqrt{6}$=$\frac{2\sqrt{6}}{3}$．
解答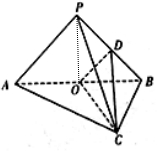 
解：（1）∵O、D分别是AB，PB的中点，∴OD∥AP
又PA?平面COD，OD?平面COD
∴PA∥平面COD．
（2）连接OP，由△PAB是等边三角形，则OP⊥AB
又∵平面PAB⊥平面ABC，∴OP⊥面ABC，且OP=$\frac{\sqrt{3}}{2}×2\sqrt{2}=\sqrt{6}$．
∴三棱锥P-ABC的体积V=$\frac{1}{3}{s}_{ABC}×OP=\frac{1}{3}×\frac{1}{2}×{2}^{2}×\sqrt{6}$=$\frac{2\sqrt{6}}{3}$．
点评 本题考查了空间线面平行的判定，棱锥的体积计算，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
19．已知不等式（m2+4m-5）x2-4（m-1）x+3＞0对一切实数x恒成立，则实数m的取值范围为（ ）
| A． | （-∞，-5）∪（1，+∞） | B． | （1，19） | C． | [1，19） | D． | （19，+∞） |
17．已知cosα=-$\frac{3}{5}$，α是第三象限的角，则sinα=（ ）
| A． | -$\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | -$\frac{4}{5}$ | D． | $\frac{4}{3}$ |
已知函数f（x）=Asinωx（A＞0，ω＞0）的图象如图所示，则A，ω的值分别是3，2．
14．
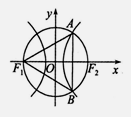F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，以坐标原点O为圆心，|OF2|为半径的圆与该双曲线右支交于A、B两点，若△F1AB是等边三角形，则双曲线的离心率为（ ）
F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，以坐标原点O为圆心，|OF2|为半径的圆与该双曲线右支交于A、B两点，若△F1AB是等边三角形，则双曲线的离心率为（ ）| A． | $\sqrt{3}$ | B． | 2 | C． | $\sqrt{3}$-1 | D． | 1+$\sqrt{3}$ |
1．下列说法正确的是（ ）
| A． | ?x，y∈R，若x+y≠0，则x≠1且y≠-1 | |
| B． | 命题“?x∈R，使得x2+2x+3＜0”的否定是“?x∈R，都有x2+2x+3＞0” | |
| C． | a∈R，“$\frac{1}{a}$＜1”是“a＞1”的必要不充分条件 | |
| D． | “若am2＜bm2，则a＜b”的逆命题为真命题 |
19．
如图所示，用A1、A2、A3三个元件连接成一个系统，A1、A2、A3能否正常工作相互独立，当A1正常工作且A2、A3至少有一个正常工作时，系统正常工作，已知A1、A2、A3正常工作的概率均为$\frac{2}{3}$，则系统正常工作的概率为（ ）
如图所示，用A1、A2、A3三个元件连接成一个系统，A1、A2、A3能否正常工作相互独立，当A1正常工作且A2、A3至少有一个正常工作时，系统正常工作，已知A1、A2、A3正常工作的概率均为$\frac{2}{3}$，则系统正常工作的概率为（ ）| A． | $\frac{4}{27}$ | B． | $\frac{8}{27}$ | C． | $\frac{16}{27}$ | D． | $\frac{20}{27}$ |