题目内容
给出以下三个关于x的不等式:①x2-4x+3<0,②
>1,③2x2+m2x+m<0.若③的解集非空,且满足③的x至少满足①和②中的一个,则m的取值范围是 .
| 3 |
| x+1 |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:分别求得①、②的解集,可得它们的并集,由题意可得,方程2x2+m2x+m=0的两个实数根都在区间[-1,3]内,令f(x)=2x2+m2x+m,则由题意可得
,由此求得m的范围.
|
解答:
解:由:①x2-4x+3<0可得1<x<3;由②
>1可得
<0,即-1<x<2;
由③2x2+m2x+m<0的解集非空,可得△=m(m3-8)>0,即m>2,或 m<0.
①②解集的并集为(-1,3),故方程2x2+m2x+m=0的两个实数根都在区间[-1,3]内,
令f(x)=2x2+m2x+m,则由题意可得
.
解得-1≤m<0,
故答案为[-1,0).
| 3 |
| x+1 |
| x-2 |
| x+1 |
由③2x2+m2x+m<0的解集非空,可得△=m(m3-8)>0,即m>2,或 m<0.
①②解集的并集为(-1,3),故方程2x2+m2x+m=0的两个实数根都在区间[-1,3]内,
令f(x)=2x2+m2x+m,则由题意可得
|
解得-1≤m<0,
故答案为[-1,0).
点评:本题主要考查集合的运算及分式不等式、一元二次不等式的基本解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
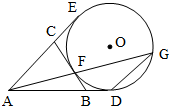 如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是
如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G,给出下列三个结论:①AD+AE=AB+BC+CA,②AF•AG=AD•AE,③△AFB∽△ADG,其中正确结论的序号是下列说法不正确的是( )
| A、所有的对立事件都是互斥事件 | ||
B、先后抛掷两枚大小一样的硬币,两枚都出现反面的概率是
| ||
| C、事件“直线y=k(x+1)过点(-1,0)”是必然事件 | ||
D、某红绿灯路口,红灯时间为30秒,黄灯时间为5秒,绿灯时间为45秒,当你到这个路口时,看到黄灯的概率是
|
设平面上有四个相异的点A、B、C、D,已知(
+
-2
)•(
-
)=0,则△ABC的形状是( )
| DB |
| DC |
| DA |
| DB |
| DC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
已知集合A={x||x+1|<1},B={x|y=
,y∈R},则A∩∁RB=( )
(
|
| A、(-2,1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
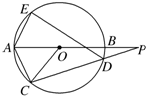 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC. 如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=
如图,矩形ABEF和正方形ABCD有公共边AB,它们所在平面成60°的二面角,AB=CB=2a,BE=a,则DE=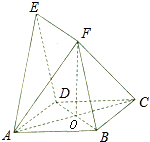 如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2
如图,四边形ABCD与BDEf均为菱形,已知∠DAB=∠DBF=60°,且面ABCD⊥面BDEF,AC=2