题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,过焦点且垂直于长轴的直线被椭圆截得的弦长为1,过点M(3,0)的直线与椭圆C相交于两点A,B.
(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足
+
=t
(O为坐标原点),当|AB|=
时,求实数t的值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)设P为椭圆上一点,且满足
| OA |
| OB |
| OP |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:综合题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)利用离心率求得a和c关系,进而利用椭圆方程中a,b和c的关系求得a和b的关系,最后利用过焦点且垂直于长轴的直线被椭圆截得的弦长求得b,则a可求,椭圆的方程可求.
(2)设出A、B、P的坐标和AB的直线方程,与椭圆的方程联立消去y,利用判别式大于0求得k的范围,利用韦达定理表示出x1+x2和x1x2,利用
+
=t
求得k和t的关系,把点P坐标代入椭圆的方程,利用|AB|=
求得k的值,进而利用k和t的关系求得t的值.
(2)设出A、B、P的坐标和AB的直线方程,与椭圆的方程联立消去y,利用判别式大于0求得k的范围,利用韦达定理表示出x1+x2和x1x2,利用
| OA |
| OB |
| OP |
| 3 |
解答:
解:(1)由已知e=
=
,所以
=
,
所以a2=4b2,c2=3b2
所以
+
=1,
又由过焦点且垂直于长轴的直线被椭圆截得的弦长为
=1,
所以b=1,
所以椭圆C的方程为
+y2=1;
(2)设A(x1,y1),B(x2,y2),P(x,y)
设AB:y=k(x-3)与椭圆联立得
整理得(1+4k2)x2-24k2x+36k2-4=0
其中△=242k4-16(9k2-1)(1+4k2)>0得k2<
,
x1+x2=
,x1•x2=
由|AB|=
=
得
=
即128k4+88k2-13=0,
所以k2=
或k2=-
(舍)
又因为
+
=(x1+x2,y1+y2)=t(x,y),
所以x=
(x1+x2)=
,
y=
(y1+y2)=
[k(x1+x2)-6k]=
,
由点P在椭圆上得
+
=4,
即36k2=t2(1+4k2),
即t2=
=9-
=3,
所以t=±
.
| c |
| a |
| ||
| 2 |
| c2 |
| a2 |
| 3 |
| 4 |
所以a2=4b2,c2=3b2
所以
| x2 |
| 4b2 |
| y2 |
| b2 |
又由过焦点且垂直于长轴的直线被椭圆截得的弦长为
| 2b2 |
| a |
所以b=1,
所以椭圆C的方程为
| x2 |
| 4 |
(2)设A(x1,y1),B(x2,y2),P(x,y)
设AB:y=k(x-3)与椭圆联立得
|
整理得(1+4k2)x2-24k2x+36k2-4=0
其中△=242k4-16(9k2-1)(1+4k2)>0得k2<
| 1 |
| 5 |
x1+x2=
| 24k2 |
| 1+4k2 |
| 36k2-4 |
| 1+4k2 |
由|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 3 |
| ||||
| 1+4k2 |
| 3 |
即128k4+88k2-13=0,
所以k2=
| 1 |
| 8 |
| 13 |
| 16 |
又因为
| OA |
| OB |
所以x=
| 1 |
| t |
| 24k2 |
| t(1+4k2) |
y=
| 1 |
| t |
| 1 |
| t |
| -6k |
| t(1+4k2) |
由点P在椭圆上得
| (24k2)2 |
| t2(1+4k2)2 |
| 144k2 |
| t2(1+4k2)2 |
即36k2=t2(1+4k2),
即t2=
| 36k2 |
| 1+4k2 |
| 9 |
| 1+4k2 |
所以t=±
| 3 |
点评:本题考查了椭圆的标准方程,考查了椭圆的简单几何性质,主要考查了直线与圆锥曲线的综合问题.解题的过程一般是把直线与圆锥曲线的方程联立,利用韦达定理和判别式来作为解题的关键.

练习册系列答案
相关题目
已知f(x)为R上的可导函数,且满足f(x)>f′(x),对任意正实数a,下面不等式恒成立的是( )
A、f(a)>
| ||
B、f(a)<
| ||
| C、f(a)>eaf(0) | ||
| D、f(a)<eaf(0) |
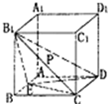 如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点. 进入2013年后全国各地雾霾天气频发,一个重要的诱因是空气中细小颗粒物.我国新引入PM2.5来衡量大气的质量.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.长沙市环保局从该市市区2013年1月份的PM2.5监测数据中随机抽取7天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
进入2013年后全国各地雾霾天气频发,一个重要的诱因是空气中细小颗粒物.我国新引入PM2.5来衡量大气的质量.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.长沙市环保局从该市市区2013年1月份的PM2.5监测数据中随机抽取7天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).