题目内容
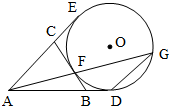如图，AD，AE，BC分别与圆O切于点D，E，F，延长AF与圆O交于另一点G，给出下列三个结论：①AD+AE=AB+BC+CA，②AF•AG=AD•AE，③△AFB∽△ADG，其中正确结论的序号是考点：与圆有关的比例线段
专题：直线与圆
分析：从圆外一点引圆的两条切线，切线长相等，得到第一个说法是正确的，根据切割线定理知道第二个说法是正确的，根据切割线定理知，两个三角形△ADF～△ADG，得到第三个说法错误．
解答：
解：根据从圆外一点引圆的两条切线，切线长相等，
有CE=CF，BF=BD，
∴AD+AE=AB+BC+CA，故①正确，
∵AD=AE，
AE2=AF•AG，
∴AF•AG=AD•AE，故②正确，
根据切割线定理知△ADF∽△ADG
故③不正确，
综上所述①②两个说法是正确的，
故答案为：①②．
有CE=CF，BF=BD，
∴AD+AE=AB+BC+CA，故①正确，
∵AD=AE，
AE2=AF•AG，
∴AF•AG=AD•AE，故②正确，
根据切割线定理知△ADF∽△ADG
故③不正确，
综上所述①②两个说法是正确的，
故答案为：①②．
点评：本题考查与圆有关的比例线段，考查圆的切线长定理，考查圆的切割线定理，考查切割线构成的两个相似的三角形，本题是一个综合题目．
练习册系列答案
相关题目
设函数f（x）的定义域为D，如果存在正实数k，对于任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”，已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2014型增函数”，则实数a的取值范围是（ ）
| A、a＜-1007 | ||
| B、a＜1007 | ||
C、a＜
| ||
D、a＜-
|
条件p：-2＜x＜4，条件q：（x+2）（x+a）＜0；若p是q的充分而不必要条件，则a的取值范围是（ ）
| A、（4，+∞） |
| B、（-∞，-4） |
| C、（-∞，-4] |
| D、[-4，+∞） |
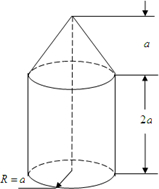图示是一个几何体的直观图，画出它的三视图．